6.3重力
【与教材不同之处】
对重力的产生原因有更详细的分析;描述了什么是“失重”;更详细描述了探究重力与质量定量关系的实验过程;更详细描述了重力的方向及应用。

实验已经证明,如图6-3-1所示,当我们在地球上搬起一块石头时,常感觉沉甸甸的。假如你在月球表面上,搬起同样的石头时,你可能会发现,这块石头的重量变轻了很多,所以,当你在地球上只能搬起一块石头时,而在月球上你却可搬起6块。什么是重力
为什么会产生如此神奇的不同体会呢?这是因为石头分别在地球和月球上受到的重力不同造成的。
那么,什么是重力呢?
物理学中,把地面附近的物体因地球的吸引而受到的力,叫做重力,用G表示。
从定义上看,重力是来自地球的引力,而不是来自物体的本身。
所以,我们觉得一块石头很重,不是因为石头本身很重,而是因为石头受到的地球的引力很大,造成了物体具有很大的重量。
如果石头在太空中某个离地球很远的地方,石头受到的地球引力变小了,这时,同样的一块石头将变得很轻。若受到的地球引力为零,石头的重量也一定为零。
所以,我们可以得到这样的结论:
(1)物体有没有重量,并不是由物体本身决定的,而是由是否受到地球的引力决定的。
(2)只有在地球表面附近的物体才受到重力。
有个有趣的现象是,即使在地球上,同一物体分别处于赤道与南北极的位置时所受的重力的大小其实并不相同。
这是因为地球本身并不是一个完美的球形,而一个扁平的㮋圆球形,这就造成了赤道表面离球心远,地球引力小;南北两极离球心近,地球引力大。所以,同一物体分别在赤道(低纬度)和北极处(高纬度)时所受到的重力也略有不同,在赤道处的重力要稍小些,在北极处的重力要稍大些。
物体受到重力时会产生什么现象
物体受到重力,会产生很多现象:
比如,我们感受到物体有重量感就是因为物体受到了重力的原因。爬山时,由于我们的身体受到了重力,所以会感受到脚很吃力;肩膀扛着包裹,由于包裹受到了重力,所以我们会感受到肩膀的疼痛;手抱着石头,由于石头受了重力,所以我们会感受到手臂又累又乏……
物体是否受到重力,并不总是依靠人的感受来体现。
当我们把石头扔下悬崖,石头由于受到重力,所以加速落向悬崖底部。
地球上的水由于受到重力,所以总是由高处往低处流。
需要说明的是,地球表面还有一层我们肉眼看不见的大气层,大气层也会受到重力作用,所以,越是靠近地球表面,空气密度越大。抛出的石头,除非能做到远离地球,否则石头由于受到重力终会落回地面。无论你在北极抛出石头,还是南极抛出石头,只要石头在地球的附近,都会受到重力终会落回地面。如图6-3-2所示。
“失重”现象
可能有人会问,天上卫星是否受到重力?月球是否受到重力?
根据重力的定义——重力是指因地球的吸引而受到的力——可知,这个定义非常的模糊。但我们知道,地球的引力产生两种效果:使物体落向地面(空中的石头)或绕地球转动的向心力(卫星绕地球转动)。
也就是说,重力和向心力都是来自地球的引力,这两个力的实质是引力的分力。或者说,引力体现为这两种力的综合。
卫星绕地球转动,向心力大,则重力小,几乎为0。月球也是如此,因此,天上卫星和月球只受到引力,但没有受到重力。
我们有些同学很喜欢蹦极,这项极限运动常会让人感受到印象深刻的“失重”。
很显然,在蹦极时,我们受到的重力并没有消失,反而是因为受到重力,我们的身体从高处加速向低处落下,跟瀑布的水在重力作用下由高处落向低处没有什么两样。
我们之所以称蹦极运动是一种“失重”现象,其实是指失去了地面的支撑作用。平时站在在地面上,由于受到地面的支撑作用,抵消了重力对我们造成的影响。当我们跳起时,立即会感受到身体在重力作用下,马上落向地面。现在蹦极时,只不过是将落下的高处变得更大一些而已罢了。
所以,蹦极不但不是“失重”现象,反而是体验只在重力的作用下而带来的加速下落时带来的一种心慌、没有实感的刺激感觉。
又比如,人坐过山车时,过山车忽然下降,这时人的重力是没变的,但过山车对人的支持力会忽然变小,这时,人极易产生一种心慌的极端感受。如果说这是一种失重现象,不如说它是重力作用带来的心慌现象。
物体如果不受重力作用时……
如果地球表面附近的物体不受重力,那么就不会出现水自高处往低流、抛出的石头将不再落回地面、地球表面也将不会被大气包裹、有些测量工具也不能使用(比如天平)……等。比如在空间站里,一切物品都不受重力作用,所以我们刚才所说的现象都会出现。
重力大小的测量
我们是如何知道不同物体所受重力的大和小的呢?
测量物体所受重力的大小,我们需要借助工具:弹簧测力计。
弹簧测力计之所以测出重力,是因为当物体吊在弹簧力计的挂钩上时,物体所受的重力越大,对挂钩的拉力就越大,弹簧的伸长的长度(伸长量)就越长。
需要注意的是,当使用弹簧测力计测量物体受到的重力时,应当让弹簧测力计沿竖直方向悬挂起来,这样就确保重力方向与弹簧受到的拉力的方向在同一直线上。
实验探究重力与质量的关系
现在,我们有个很有趣的问题要探究:一个物体的质量成倍数增大时,它受到的重力是不是也会成倍数增大,也就是重力与质量是否成正比例关系?
现在我们来通过实验来探究这个问题,实验前的准备工作包括:
(1)器材准备:测量工具可以是天平和弹簧测力计,选择多个规格相同的钩码作为实验对象。

为什么要设计表格呢?(2)记录数据的表格设计:
采用列表的方法记录各种数据,便于分析对比,有利于发现事物发生、发展的规律。因此,表格的使用也是进行科学探究的有效方法。
如何设计表格?
由于表格应当具有可读性,所以初中物理的表格的设计是有规范要求的。比如,表格的项目栏必须包括包含物理量符号的项目名和物理量的单位,本次实验中要记录的测量的物理理是质量和重力,所以表中参数为“钩码的质量m”和“钩码的重力G”,单位分别是“kg”、“N”。
用天平先测量一个钩码的质量,接着用弹簧测力计测量出这个钩码的重力,并将数据记录在设计好的表格中。(3)设计实验步骤:
- 多次改变钩码的质量,重复步骤(1)的操作。
按上述步骤进行实验后,我们收集了多组的实验数据。为了判断重力大小与质量之间是否存在正比例关系?我们需要将求出重力大小与质量的比值。你可能会发现,每组实验所测得的重力与质量的比值并不相同。
重力大小与质量大小比值虽不同,但总是相差不大,这是什么原因呢?是不是因为测量工具的误差造成的呢?我们发现,弹簧测力计测量重力大小时的误差有些大(因为实验室里最精确的弹簧测力计分度值也只有0.1N),所以,我们为了提高测量重力大小的数据的准确性,我们可选择数显测力计(如图6-3-3所示),它的工作原理与普通弹簧测力计原理相似,但它的分度值可以达到0.01N,可以满足本实验的需要。

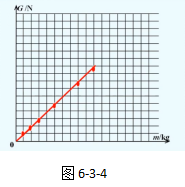
改进实验器材后重复上述实验,如图6-3-4所示。

这时我们将测得的重力大小与质量相比时,发现比值的差异的确缩小了,基本稳定在9.8N/kg左右,这说明,比值之所以不同,的确是因为误差造成。如果没有误差,重力大小与质量的比值一定是定值。
为了直观的判断重力的大小与质量的比值否是一个定值,我们可借助坐标图来进行分析。因为坐标图既形象直观 ,又便于分析实验误差 ,有助于正确理解坐标图线所表达的相应规律及现象的物理意义。于是,我们通过先描点再画线的方式,结果得到一条经过倾斜的直线。图6-3-4,就是某次实验数据整理后得到的坐标图。
在误差允许的范围内,我们将这个定值指定为9.8N/kg。于是,我们有这么一个数学关系:
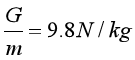
所以,我们完全可以得出结论:物体的重力大小与其质量成正比。
我们用g来表示9.8N/kg,所以,得到这么一个等式:
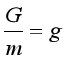
重力公式的应用
我们将公式G/m=g变形,于是我们可以得出一个常用的求重力大小的公式:
![]()
如果不特别指出,g值的大小一般采用9.8N/kg。
但在粗略的计算中,g可取10N/kg。
例题:若一个中学生的质量是50kg,那么他的重力是多少?(g取10N/kg)
已知:m=50kg g=10N/kg
求:G
解:
![]()
答:中学生的重力是500N。
如果我们这个实验在月球上进行,那么你测得的比值g会变小很多,是地球上g值的六分之一。这是因为整个地球对物体的引力是整个月球对物体引力的6倍。
判断重力的方向

如图6-3-5所示,苹果之所以向下落,滑雪运动员之所以能沿坡面向下滑,都是因为受到了重力的作用,那么,能不能说物体受到重力的方向与物体的运动方向一致呢?我们已经知道了重力的大小与质量成正比, 那么整个地球对物体施加了重力后,重力指向何方?
如果重力方向与运动方向完全一致的话,那么滑雪运动员对斜面的压力也是来自重力,这怎么解释呢?重力的方向倒底指向何方呢?所以,以运动方向来判断重力方向并不可靠。
那么以什么方法来判断重力的方向呢?
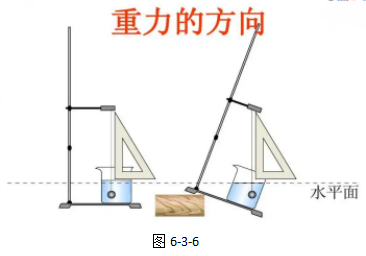
我们将线所在方向与烧杯中的水平面作比较,发现拉直的线始终与水平面垂直。如图6-3-6左图所示,当把一个物体悬挂起来保持不动时,此时的物体一定只受到两个力,一个是沿直线向上的拉力,一个是重力,根据二力平衡(后面会学到),拉力与重力方向相反。也就是说,线拉直时,沿着线向下的方向就是重力方向。当我们改变把铁架台的一段垫高,线的方向(即重力的方向)不会发生改变。
垂直于水平面方向我们称为竖直方向。
所以,我们得到的结论是:重力的方向总是竖直向下的。
重力的方向的应用
现在我们知道了线的下端吊着重物时,线所在的方向总是竖直方向。所以,我们将一条细线悬挂一个金属重物的装置称为重垂线,也叫铅垂线。

重垂线装置虽然简单,但作用巨大。在建大楼的时候,工人师傅就是重锤线来检验墙壁建造的是否竖直,如图6-3-7。这就是重力方向在生产中的一个典型应用。不仅重重线利用了重力的方向总是向下的道理,水平仪(图6-3-7中右图)的原理也是利用重力的方向总是向下的道理。若水平仪中的重物偏向右边,表示右边的位置较低。
重力的作用点的研究

如果这是一块规则、质量均匀分布的木板,支撑起这块木板的位置会正好在其对角线交点,也就是在长方形木板的几何中心上。我们来做一个小实验,如图6-3-8,用一根平头的小棍如何将一个长方形木板支撑起来?
一个支撑点就可以将整个木板支撑起来的事实告诉我们,整个物体受到的重力可以看成作用在物体的某个点上,这个点叫做重心。
我们需要注意的是,重心只是一个等效作用点。因为木板的每一部分都受到地球对其施加的重力,也就是说,木板的每一部分都是重力的作用点,我们只是为了研究问题的方便性,我们设定整个物体受到的重力都集中到了一个等效作用点上。

对于形状不规则、质量分布不均匀的物体,它的重点如何确定呢?既然重心是一个等效作用点,重心可能不在物体上(作用点一定是在物体上的,但由于重心只是等效作用点,不是真实的,所以它可能不在物体上)。比如图中的金属环,它的重心就位于金属环的圆心上,并不在金属环上。类似的还有足球、篮球等中空的物体,显然重心都不在物体上。
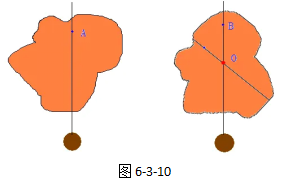
我们可以用悬挂法,如图6-3-10所示,根据重垂线原理,悬挂点与重心一定在同一条竖直直线上。因此,过A点和B点的重垂线的交点就是重心的位置。
重心位置与稳定性的关系
所谓稳定性,是指物体倾倒的难易程度。
当我们支撑点正好竖直对准了重心(即支撑点与重心在同一条竖直直线上),则物体就会稳稳地立在那里,不会倒下。如图6-3-11所示,这块岩石没有倒下,就是因为支撑点竖直对准了重心。

如果不止一个支撑点,而是一个支撑面。那么我只要确保过重心的竖直直线在支撑面的范围以内,物体仍是可以保持稳定,不会倒塌的。比萨斜塔至今没有倒塌,就是因为斜塔的重心所在的竖直直线仍在支撑面的范围以内,如图6-3-12所示。

我们需要注意的是,支撑面的大小与受力面积的大小是有区别的。比如,图6-3-13中,小树和扶架的受力面积很小,但它们构成的支撑面积很大,所以,小树的稳定性大大增强,不会轻易地倾倒。

所以,一个物体的稳定性与支撑面积的大小有关,支撑面积越大,物体的稳定性越高。通过降低重心的位置也可以增加物体的稳定性。比如,赛车的车身低矮,就是通过降低重心的高度从而增强稳定性。赛车的车轮宽大,有利于增大支撑面积从而增加稳定性。
【本节学到的内容】
1、什么是重力?
把地面附近的物体因地球的吸引而受到的力,叫做重力,用G表示。
2、重力大小与质量的关系
物体的重力大小与其质量成正比,公式为:
3、重力的方向
重力的方向总是竖直向下的。
4、重心的位置
形状规则、质量均匀分布的物体,重心在它的几何中心上。
5、稳定性与重心位置的关系
增大支撑面积,降低重心高度,都可以增强稳定性。
【课后巩固习题】
1、如图所示是正在太空中运行的我国空间实验室“天宫二号”。在完全失重的“天宫二号”里,下列实验可以完成的是( )
- 轻易地往水杯中倒水
- 让铁球悬浮在空中
- 用弹簧测力计测重力
- 用刻度尺测书本的长度
2、璀璨的历史文化是文旅行业发展的宝贵财富,如图为“大唐不夜城”的不倒翁表演。 在演员倾斜的过程中她所受重力的( )

A.大小不变,方向改变 B.大小不变,方向不变
C.大小改变,方向改变 D.大小改变,方向不变
Was this helpful?
1 / 0