洛仑兹变换方程,我们都已经熟悉了吧。“静止”的观察者(地球上)测得的位置和时间(x,y,z,t)和在以速度u“运动”的宇宙飞船里的观察者测得的相应的坐标和时间(x’,y’,z’,t’)之间的变换(或者叫修正)符合下方的方程组:
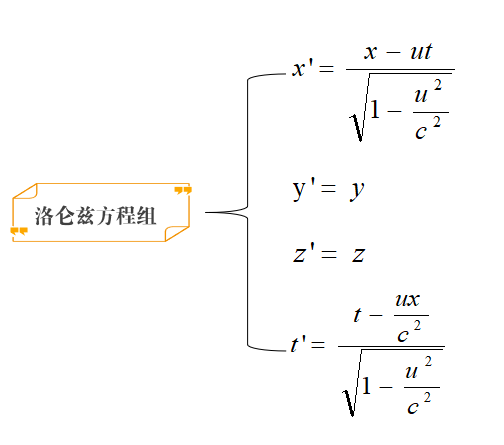
这个方程组将给我们更深的启示。
我们知道,
一个坐标系相对另一个坐标系作转动时,新坐标与旧的坐标的关系符合下列关系:

上面的式子让我们看到,新的x’是旧的x和y的混合。
我们能否用同样的方式来看洛仑兹变换?这里新的t’也是旧的t和x的混合,t代表时间,x代表空间。
也就是说,空间量度与时间量度的差值产生了一个新的空间量度。
换句话说,
某人的空间量度,在另一个人看来,却掺入一些时间的量度。
又举个例子,


只看左图中的花瓶,我们知道物体有一个确定的深度,但看了右图后,左图中确定的视深度其实可以是右图中视宽度与视深度的一种混合。
如果我不能移动位置,那么我只能看到左图或右图,我们会认为宽度与深度是完全不同的性质,因为一个表现为视张角,另一个与眼睛聚焦有关。
我们会认为宽度与深度是非常不同的事物,永远不会混合。
上面的例子与我们只能在普通的空间世界里看某物体的情形有些相似。
因为,我们只能在地球上看见客体,而不能乘坐在接近光速的飞船上来看此物体,犹如不能移动位置从不同的角度来观察同一物体一样。
所以,我们认为时间与空间也是非常不同的事物,永远不会混合的两种性质。
但如果我们能从高速飞船上看相同客体时,相当于我们从不同的角度来观察同一物体一样,就会发现:
某人的空间量度,在另一个人看来,却掺入一些时间的量度,即某人的空间量度是新的空间量度和新的时间量度的混合。
飞船上的空间量度为x’,飞船的速度为u,地球上的空间量度为x,地球上的时间量度为t,则
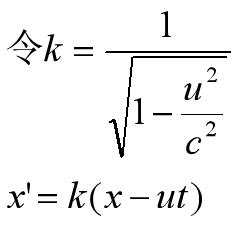
上式中,我们很明显看到,飞船上的空间量度的确是可以由一种空间和时间混合在一起的新的世界想象客体。这个客体跟目前我们看到的客体是一样的事实存在。
如果我们以不同的速度运动,相当于我们能从不同的角度观察这个几何实体,只不过这个几何实体占有位置并包含一定的时间。
我们还发现,飞船的时间量度t’,也可以由地球上的空间量度x和地球上的时间量度t混合,式子如下
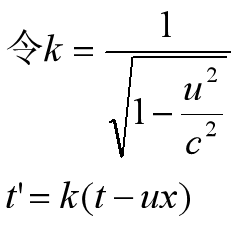
这个新的世界为“时空”。
新时空的坐标与地球上的时空坐标关系如下:
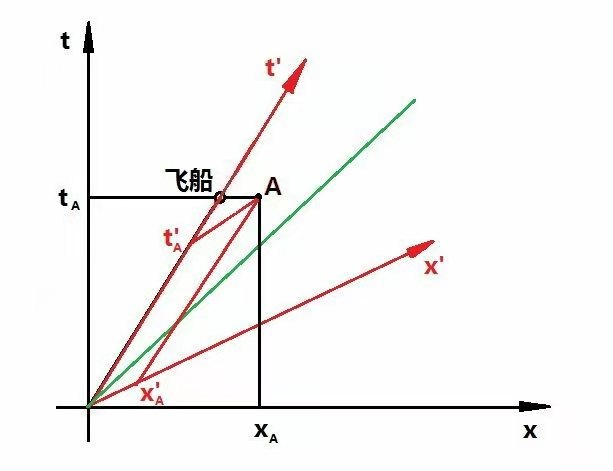
上图中,一艘飞船从原点o出发,以速度u在运动,飞船上某物体以某速度v’运动到A点。
为了讨论t’和x’的坐标如何画出,我们令式子
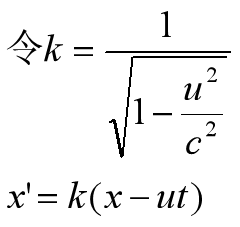
中的x’=0,则得到
x=ut
此条线表示新时空世界的时间轴t’。
此条时间轴t’表示相对飞船上静止的物体随时间流逝而位置x’始终为零,且不发生改变。与地球坐标系中的x=0的意义是一样的。地球上的时间轴t也是物体相对地球静止时。所以,x=0和x’=0分别是地球的时间轴和飞船系统的时间轴。
我们再令式子
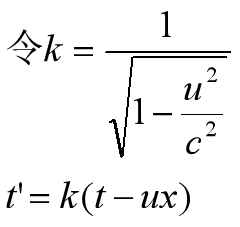
中的t’=0,则得到
t=ux
此条线表示新时空世界的空间轴x’。
此条空间轴x’表示物体移动到任何位置却没有花费时间,与地球坐标系中的t=0的意义是一样的。地球上的时间轴t也是表示物体出现到任何位置却没有花费时间。很明显,这条线是表示多物体的空间关系。所以,t=0和t’=0分别是地球的空间轴和飞船系统的空间轴。
如果以s来表示0与A的间隔,则必有
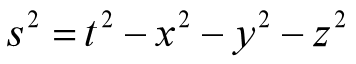
因为S2>0,代表A事件与0事件在世界线以内,事件之间有因果有关系,原点与A的点的距离(或间隔)叫类时间隔。
若S2<0,代表A事件与0事件在世界线以外,事件间不可能有因果有关系,是两件完全独立的事,原点与A的点的距离(或间隔)叫类空间隔。
若S2=0,只有一条线,这条线叫类光间隔。这条线是类空间隔与类时间隔的分界线,也就是世界线。
在两条世界线围成的光锥范围内(以时间轴为对称轴)是类时间隔,事件之间是存在因果关系的。
在两条世界线围成的光锥范围外(以空间轴为对称轴)是类空间隔,事件之间并不存在因素关系。
Was this helpful?
0 / 0