6.6 探究滑轮的作用
【与教材不同之处】
更详细分析了动滑轮是否省力;更详细描述了滑轮或滑轮组中的两种距离的关系;更详细描述了水平滑轮组的省力、费距离情况;更详细描述了轮轴、斜面等机械。
什么是滑轮
什么滑轮?
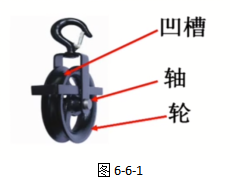 这种周边有槽、绕轴心转动的圆轮叫做滑轮,如图6-6-1所示。
这种周边有槽、绕轴心转动的圆轮叫做滑轮,如图6-6-1所示。
什么是定滑轮

如图6-6-2所示,如果我们将轴心固定,滑轮绕上绳索,那么,滑轮将在绳索的带动下绕轴心转动的。绕在滑轮上的绳索一端系住重物,另一端由人或可施加动力的机器拉着。当我们拉动绳索,重物在拉力作用下运动起来。
这种轮转动但轴心的位置固定不动的滑轮,叫着定滑轮。
为什么要使用定滑轮
我们不禁有个疑问,我们本可以直接用绳索来拉动物体,为什么还要将绳索绕在滑轮上再来拉动物体呢?
我们来做一个实验,来观察使用滑轮时,相比我们对物体直接施加拉力时会有什么不一样的地方?如图6-6-3所示。
通过比较发现,没有滑轮时,通过绳索提升重物时,施力的方向必须是竖直向上。
借助定滑轮后,我们提升物体时,拉力的方向不再是竖直向上。拉力方向可以是向下的,或者斜向下的……,也就是说,这个滑轮帮助我们改变了拉力的方向。而改变拉力的方向的好处是:使施力的方式更方便。

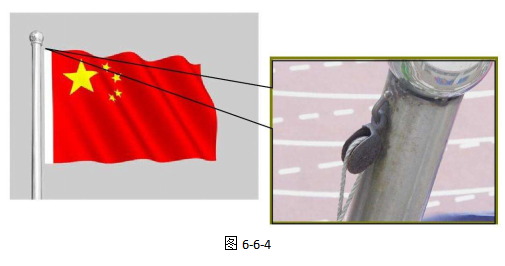
又如,我们升国旗时,没有滑轮时,我们可能需要爬到杆顶,站在杆顶将国旗拉上去,此时的拉力方向是竖直向上的。而有了定滑轮,我们站在地面上,向下施加拉力,国旗也可以被提升至杆顶,很明显,使用定滑轮让我们施力的方式更方便简单。如图6-6-4所示。比如,从深井中打水,没有定滑轮时,只能靠双手向上提起绳索,不仅容易打滑,而且辛苦;而有了滑轮,我们可以向下施加拉力,这种方式可以方便我们利用体重来施加对绳索的拉力,我们还可以沿着某个方向一边走一边拉,不需要交替用手,防止打滑。
所以,我们使用这种轮转动但轴心不动的定滑轮,最大的目的就是为了改变拉力的方向。
使用定滑轮是否省力
定滑轮在改变拉力方向的同时,有没有改变拉力的大小呢?
我们用弹簧测力计测出图6-6-3中各种情形的拉力大小,并记录在下表中。
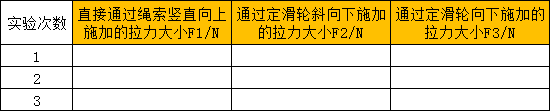
这就说明,使用定滑轮后,拉力大小并没有减小,仍与原来直接施加在物体上的拉力大小相同。如果考虑绳重、滑轮与轴心之间的摩擦的影响,拉力还会比物体重力更大。我们发现,在摩擦力和绳子重量很小可以忽略不计的情况下,三种情形中的拉力大小是一样的,即
![]()
所以,使用定滑轮不可能省力。所谓不省力,是指通过定滑轮施加的拉力,等于或大于物体重力的现象。
使用定滑轮是否省距离
定滑轮不省力,它省不省距离?
所谓省距离,是指绳子的自由端移动的距离比物体被拉动的距离小。
什么是绳子的自由端?
定滑轮上绕了一根绳子,这根绳子有两个端点。一个端点挂着重物,另一个端点施加一个外来的拉力。外来的拉力作用的端点就叫着绳索的自由端。
如果把重物对绳索的拉力称为阻力,那么外来的拉力(比如人施加的拉力)就称为动力。所以,省距离也可以说成是动力(或外来的拉力)移动的距离比物体自身移动的距离小的现象。
我们利用前面的装置再做几遍实验,只不过,这几次我们要测量一下物体上升的高度h和拉力向下运动时移动的距离s。
通过比较h和s,我们发现,
![]()
这就说明,使用定滑轮也不省距离。
定滑轮是不是等臂杠杆
我们不由地联想起前面我们学过等臂杠杆,比如天平,它的特点是不省力也不省距离。
难道定滑轮也是一种等臂杠杆?
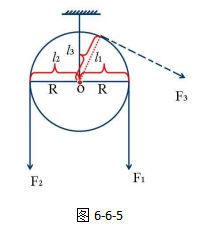
从图中,我们可以看出,滑轮的支点在轮的轴心处,轮的半径就是力臂,也就是说,动力臂与阻力臂始终相等。改变拉力的方向,动力臂与阻力臂相等的关系并不会发生改变。如图6-6-5所示,定滑轮的外形看上去的确不是一根细杆状,但仍可以将定滑轮看成一根杠杆,只不过是“变胖”的杠杆。
所以,使用定滑轮时,在理想情况下,动力与阻力的大小是相等的。即定滑轮不会省力,也不会省距离,定滑轮其实是一个变形的等臂杠杆。
什么是动滑轮
使用滑轮难道只能是定滑轮的方式?
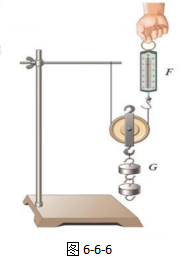
当我们提升轮上某边的绳索时,重物也会上升,而且滑轮也会随之上升。这时的重物与滑轮犹如一个整体,它们提升的高度、快慢始终是一样的。如果我们将定滑轮倒置过来,我们有趣地发现,滑轮也可以由绕在轮上的两股绳子吊起来,重物则可挂在轴心上,如图6-6-6所示。
这种会与重物一起运动的滑轮,叫着动滑轮。
我们发现,使用动滑轮后,提升物体的拉力的方向仍旧是向上的。也就是说,以动滑轮的方式来提升物体,并不能改变拉力的方向。
所以,我们要改变拉力的方向时,总是采用定滑轮的方式,而不是采用动滑轮。
动滑轮省力吗
那么,动滑轮会不会跟定滑轮一样不省力呢?
我们通过实验来探究使用动滑轮是否省力?
我们用弹簧测力计分别测量出绕在动滑轮上的拉力大小和挂在动滑轮的轴心上的物体重力大小,并将数据记录到下表中。

这就说明,使用动滑轮,的确可以实现用较小的拉力却可提升更重的物体。即,使用动滑轮省力。通过数据,我们发现,若动滑轮的重力、摩擦力和绳子重量都很小,拉力F非常接近物体的重力的二分之一,即
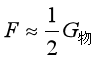
例如,通过动滑轮,当我们施加的拉力为10N,却可提升起近20N的物体,这种现象就是省力。
动滑轮省距离吗
动滑轮省力,它省不省距离?
我们利用图6-6-6的装置,准确测量物体上升的高度h和拉力向下运动时移动的距离s。
通过比较h和s,我们发现两者存在准确的定量关系,
![]()
多测量几组h和s数据,上述等式仍然成立。这就说明,使用动滑轮费距离的,即拉力向下运动时移动的距离比物体上升高度大,而且拉力向下运动时移动的距离s比物体上升高度h的两倍。
动滑轮省力费距离的特点与我们在上个章节学的省力杠杆的特点非常相似,难道动滑轮的本质就是一个省力杠杆?
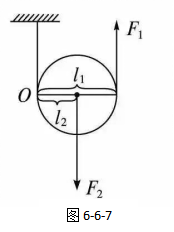
我们对动滑轮的结构进行简化,得到如图6-6-7。
从这个图中,我们发现,动滑轮在工作时,其实是绕O点转动的,这时,如果拉力沿着竖直向上的方向拉动,则动力臂是直径,阻力臂是半径,动力臂是阻力臂的2倍。
现在,我们终于知道了动滑轮可以省力的原因了。因为根据杠杆平衡条件,当动滑轮的动力臂是阻力臂的2倍,动力就是阻力的一半,即动滑轮可以省一半力。
动滑轮省力情况进一步分析
当然,动滑轮省一半的力时,我们是忽略了动滑轮的自身的重量的,也忽略了绳重、摩擦等因素,即在理想情况下,使用动滑轮提来工作,可以省一半的力。
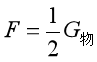
如果动滑轮自身的重力比较大,不能忽略时,我们则可以将动滑轮看成重物一部分,则有
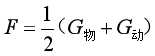
需要注意的是,如果拉力的方向是斜向上,则它的力臂是一段弦,比半径大但比直径小,也就是说,只有拉力的方向是竖直向上时,力臂是直径,此时的力臂是最大的,拉力也是最小的。这样的动滑轮才最省力,理想时,才可以省一半力的。
动滑轮一定省力吗
根据上面我们推导的公式
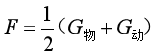
可知,当动滑轮的重量比物重还要大时,则该动滑轮不能省力,反而费力。
比如物重是10N,动滑轮重20N,若此时使用动滑轮来提升物体,则拉力F为15N,比不使用动滑轮时直接提升物体所施加的拉力10N还要大。
所以,在现实中,动滑轮是否省力,还要关注动滑轮的自重的大小是否比物重要小。
最后要强调的是,使用动滑轮并不能改变拉力的方向。
因为没有动滑轮,我们提升物体的拉力是向上的,有了动滑轮,通过刚才的分析,我们通过动滑轮提升物体的方向仍然是向上的。
什么是滑轮组
看来,定滑轮和动滑轮都有优点和缺点,那么,我们能不能将滑轮的这两种工作方式组合起来,以便这样的装置工作时既可以省力,又可以改变拉力的方向?
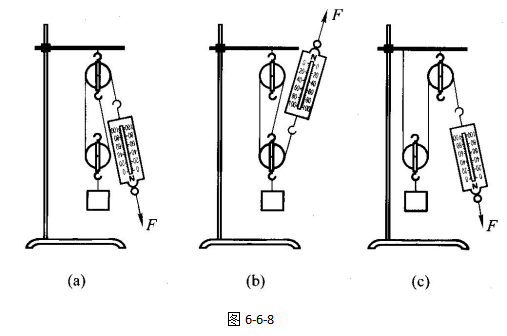
为了将一个定滑轮和一个动滑轮组装成可以工作的多滑轮装置,我们可以通过不断尝试,最终,我们有如图6-6-8所示的几种不同的组合。
像这种由定滑轮和动滑轮组装而成的机械,叫做滑轮组(或称复式滑轮)。
滑轮组省力情况的分析
滑轮组既然是由定滑轮与动滑轮组合而成,而且有多种组合方式。
那么,不同的组装方式的省力情况是否相同呢?
我们将这几种不同的组装方式提升相同重量的钩码,再用弹簧测力计分别测量出作用在绳子自由端上拉力的大小F,并将拉力大小记录在表格中。
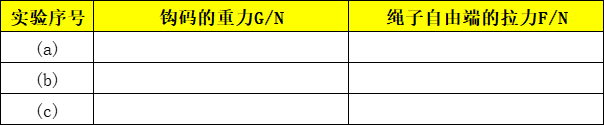
将拉力大小与钩码的重力大小比较,我们发现:
(a)图中拉力大小接近物重的二分之一;
(b)图的拉力大小接近物重的三分之一;
(c)图中的拉力大小接近物重的二分之一。
为什么(a)和(c)图的拉力大小是一样的,而(a)和(b)图中拉力大小不一样呢?
我们知道,定滑轮是不省力不费力的杠杆,所以,几种不同的组装方式中出现的拉力不同,应当是由动滑轮的绕线情况决定。通过观察发现,
(a)和(c)图中动滑轮上绕线有两股(或称为两段),它们的拉力是一样的,拉力大小都接近物重的二分之一;
(b)图中动滑轮的绕线是三股,拉力大小恰好接近物重的三分之一。
于是,我们不难推断:滑轮组的省力情况是由动滑轮上的绕线的股数决定的。
若不计动滑轮重、绳子自重和摩擦等,且定滑轮与动滑轮之间的绳子较长,则有:
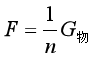
其中,n表示绕在动滑轮上的绳子的股数。
如果动滑轮的自重不能忽略,则我们可以将动滑轮当成物体重量的一部分,则上式变为:
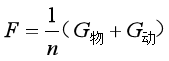
通过上式,我们知道了滑轮组省力的奥秘:若想滑轮更省力,就应该想方设法增加滑轮组中动滑轮上的绳子的股数。
所以,如图6-6-9所示,这个起重机上装有滑轮组,而且这个滑轮组的动滑轮上绳子的股数有6股,这说明,当这个起重机的动力为10000N时,却可以提升起近60000N的重物。

滑轮组省距离吗
现在,我们已经知道了滑轮组的省力特点,但是,我们还不知道滑轮组是省距离还是费距离?
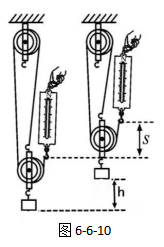
我们借助6-6-10的装置,利用刻度尺来测出s和h的大小,并将相应的数据填入下表中。也就是说,我们还有必要探究滑轮上的绳子自由端移动的距离s与被提升的物体上升的高度h的关系。
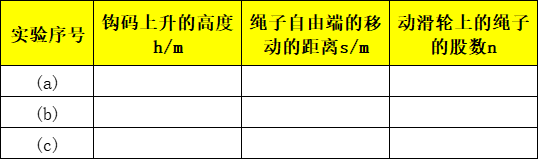
即,若动滑轮上的绳子的股数是n,则绳子自由端移动的距离是重物上升高度的n倍。通过对表中的数据分析,我们可以得到s、h和n之间的关系式:
![]()
由于绳子自由端的移动和重物的上升是同时开始,同时结束,也就是,这两段距离所用的时间是一样的。所以,上式的两边同时除以时间,我们更可以推导出绳子自由端移动的速度(或者称为拉力移动的速度)v拉与重物上升的速度v物之间满足这么一个等式:
![]()
水平方向使用滑轮组的不同之处
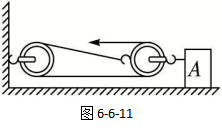
我们先看一个使用水平滑轮组来拉动一个物体的简化图,如图6-6-11所示。其实,滑轮组不仅可以用于竖直方向提升重物,还可以水平方向拉动物体。那么,在水平方向上使用滑轮组与竖直方向上使用滑轮组有什么相同和不同之处呢?
水平方向使用滑轮组,阻力应当仍然是动滑轮的轴心上受到的拉力。很显然,当我们向右施加拉力来拉动滑轮组的自由端时,物体也会被拉动。如果是匀速拉动,则动滑轮的轴心对物体的拉力与物体受到地面的摩擦力是一对平衡力。也就是说,动滑轮受到的阻力F2的大小等于地面对物体的摩擦力f摩,则:
![]()
所以,竖直滑轮组与水平滑轮组受到的阻力的来源有可能是不同的。
我们已经探究了竖直滑轮组的省力情况,并得到如下表达式
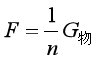
现在,我们知道了,上面的表达式其实应该写成:
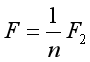
其中F指的是作用在滑轮组上并使滑轮组完成工作目标的外力(或称动力),而且f是滑轮组受到的阻力。若水平滑轮组的阻力来自于摩擦,所以,水平滑轮组的省力情况如下:
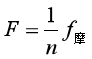
所以,图6-6-11中的拉力若是9N,则物体在水平面上滑动时,受到的滑动摩擦力为
![]()
由此可以看出,水平滑轮组与竖直滑轮组的最大区别是阻力的来源可能不同。
水平滑轮组的应用
水平滑轮组在生活中是否有应用?
在高压线的线索拉紧时,此时滑轮组的使用方式往往是水平方向的,如图6-6-12所示。
图中左边的滑轮是动滑轮,右边的滑轮是定滑轮。很明显,图中动滑轮上绕线是3股,动滑轮的框架(轴心与框架总是连在一起的)受到的高压线的拉力是阻力F2。而该水平滑轮组受到的动力F来自一叠悬吊的圆盘水泥块通过绳索对滑轮组的定滑轮的拉力。所以,根据

我们可知,电路的高压线的拉力(阻力)的大小是由水泥块的重力(动力)的n分之一。所以,通过调整水泥块的重力就能调整高压线的拉力。
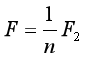
关于水平滑轮组的计算
例:图6-6-12中的每个水泥块重390N,共悬挂20个水泥块。滑轮组对高压线的拉力是多大?
解:因为滑轮组对高压线的拉力与高压线对滑轮组的拉力是一对相互作用力,而高压线对滑轮组的拉力是阻力,水泥块的重量对滑轮组的拉力是动力,则该题其实求的是阻力F2。则有
![]()
答:滑轮组对高压线的拉力是1170N。
反向动滑轮
现在,我们已经知道,滑轮组无论是竖直使用,还是水平使用,都是反映了动力与阻力的关系。但需要注意的是,动力并不总是阻力的n分之一,比如反向动滑轮,如图6-6-13中的图2。
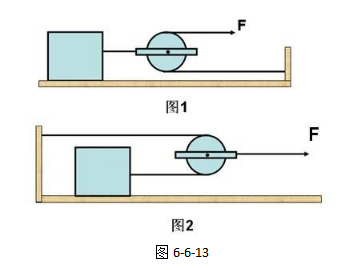
这就是说明,动滑轮并不总是省力的。
动滑轮是省力还是费力,不是看滑轮是否随物体一起运动,而是看作用在动滑轮上的动力(外来拉力)是作用在动滑轮的轮上还是轴心上。
当动力作用在轮上,是省力的动滑轮;
当动力作用在轴心上,是费力的动滑轮。
图1和图2中滑轮都是动滑轮,因为当拉力F对滑轮起作用时,物体和滑轮都会沿着拉力的方向运动。
如果不仔细观察,我们也许会认为图1和图2的动滑轮的省力情况是一样的。
但仔细观察后发现,
图1中的拉力F作用在轮上,而图2中的拉力作用在轴心上,这就意味着,图1中的拉力的力臂是直径,是阻力臂的两倍,是省力的动滑轮;
而图2中的拉力的力臂只是半径,阻力臂是直径,动力臂是阻力臂的二分之一,是费力的滑轮,所以,图2的动滑轮称为反向滑轮。
关于反向动滑轮的计算
在生活中,反向动滑轮并没有实际应用,但通过对反向动滑轮的分析,能让我们对动滑轮的省力原理有了更深刻的认识。
例:图6-6-13中图1和图2的拉力F均为10N,物体在水平木板上均移动了2m,请问
(1)物体在水平木板上受到的摩擦力分别是多少?
(2)拉力F分别移动了多少米?
解:图1中的动力F作用在轮上,阻力(即摩擦力)作用在轴心上,滑轮是省力的动滑轮,则F=1/2f,所以,
![]()
由于是省力,所以费距离,又因为物体移动的距离是阻力移动的距离,所以,动力F移动的距离是阻力移动距离的2倍,则
![]()
图2中的动力F作用在轴心上,阻力(即摩擦力)作用在轮上,滑轮是费力的动滑轮,则F=2f,所以,
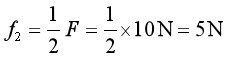
由于是费力,所以省距离,所以,动力F移动的距离是阻力移动距离的二分之一,则
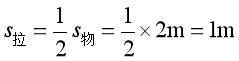
答:图1中物体受到的摩擦力为20N,拉力F移动的距离是4m;图2中的物体受到的摩擦力为5N,拉力F移动的距离是1m。
什么是轮轴
杠杆、滑轮都是简单机械,它们还可以变形为轮轴。
什么是轮轴呢?
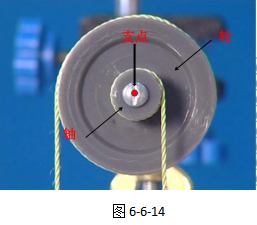
轮轴是指由“轮”和“轴”组成的能绕轴心旋转的一种简单机械,如图6-6-14所示。
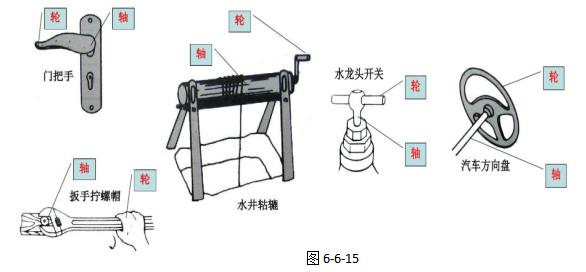
生活中有很多机械就是属于这种省力的轮轴,像门把手、扳手、水井轱辘、水龙头、汽车方向盘、螺丝刀等,如图6-6-15所示。
显然,轮轴可以看成是以轴心为支点,半径为杆的杠杆,属于不等臂杠杆。
绳分别绕在轮上或轴上,假设“轮”上的绳受到的拉力为动力,则动力臂为“轮”的半径;与此对应的“轴”上的绳受到的拉力为阻力,阻力臂为“轴”的半径。
由于轮的半径比轴的半径大,即动力臂大于阻力臂,则此时的轮轴是省力的,相当于省力杠杆。
轮轴可以省力(动力在轮上),也可以费力(作用在轴上)
因为动力作用在轴上时,动力臂是轴半径,阻力臂是轮半径,则动力臂小于阻力臂,根据杠杆平衡条件,动力将大于阻力,费力。
生活中有没有费力的轮轴?
像汽车上的雨刮器就是一个费力的轮轴,如图6-6-16所示。

凡是费力的杠杆,都会省距离。所以,当使用费力轮轴时,目的是为了能省距离。
斜面也是一种简单机械
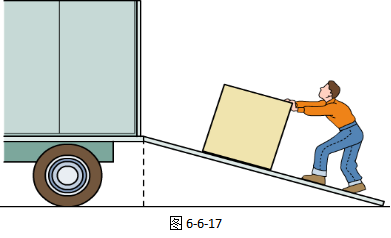
斜面的工作特点是:当高度相同时,斜面的斜面越长,越省力,但推力通过的距离也越长,简单地说:斜面省力,但费距离。斜面是一种倾斜的平板,能够将物体以相对较小的力从低处提升至高处,它也是一种简单机械,如图6-6-17所示。
为什么斜面越长会越省力呢?
斜面省力的原理不是杠杆原理,而是机械功原理(后面会学)。

生活中盘山公路,螺丝钉的纹路利用的都是斜面这种简单机械,如图6-6-18所示。
【本节学到的内容】
1、什么是定滑轮?什么是动滑轮?
这种轮转动但轴心的位置固定不动的滑轮,叫着定滑轮。这种会与重物一起运动的滑轮,叫着动滑轮。
2、定滑轮的特点、原理、用途是什么?
特点:通过定滑轮施加的各方向的拉力大小相等,且都不省力。原理:等臂杠杆。用途:改变拉力的方向。
3、动滑轮的省力特点、原理、用途是什么?
动滑轮的省力特点是:
(1)理想状态下,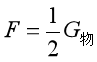 。
。
(2)动滑轮自重不能忽略的半理想状态,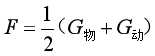 。
。
动滑轮的原理:省力杠杆。
用途:省力
4、滑轮组的省力规律、费距离规律
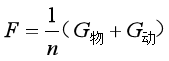
![]()
5、水平滑轮组的省力规律
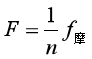
6、正向动滑轮与反向动滑轮的区别
正向动滑轮:动力作用在轮上,阻力作用在轴心上,省力,但费距离;
反向动滑轮:动力作用在轴心上,阻力作用在轮上,费力,但省距离。
【习题检测与巩固】
1、(多选)图中,用滑轮或滑轮组将重为的物体匀速拉起,不计滑轮、绳重以及轮与轴间的摩擦,绳端拉力F等于物重一半的是图中的( )
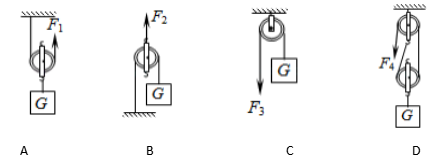
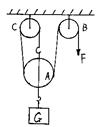
2、如图所示装置,不计拉线质量及滑轮转动摩擦影响,滑轮A重40N,滑轮B、C各重20N,重物G=200N。求:绳自由端在力F作用下,恰能以0.6m/s向下运动,则力F的大小是多少?重物G在1min内能上升多少距离?(绳子足够长)
Was this helpful?
1 / 0