11.3 如何提高机械效率
【与教材不同之处】
更详细描述有用功,额外功,总功概念,更详细描述三大机械的机械效率的求解,更详细分析机械效率的影响因素。
有用功、额外功、总功
如图11-3-1所示,当我们用桶从井中打水时,在拉力作用下,我们对水和桶都做了功。

其中,对水做功是我们需要的,有价值的功。物理学上,人们有价值的功叫做有用功,记作W有用。
打水时,我们将不得不同时将桶拉起,所以,对桶做的功其实是我们不想做的,是多余的,但又不得不做的功。像这类不需要,但又不得不做的功,我们称为额外功,记作W额外。
物理学上,有用功和额外功的总和叫做总功,用W总表示。
![]()
使用机械时的有用功
如图11-3-2所示,我们使用滑轮组提升一个物体,在此过程中滑轮组的有用功、额外功、总功分别指的是什么?
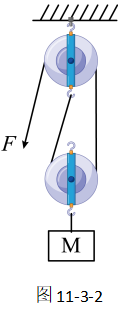
此滑轮组运作的目的是什么?
把重物提升到某一高度。
我们知道,重物被提升的过程,其实是重物克服重力做功的过程。
也就是说,此滑轮组的有用功是指重物克服重力做的功。
因此,有用功的大小为:
![]()
其中G为物体的重力,h为物体上升的高度。
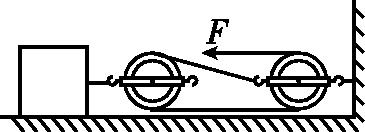
如图11-3-3所示,我们利用滑轮组水平拉动一个物体前进。
此滑轮组运作的目的是什么?
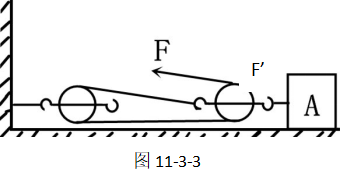
我们知道,物体在水平移动过程中,其实是物体克服地面摩擦力做功的过程。把物体水平移动一段距离。
也就是说,此水平放置的滑轮组的有用功是指物体克服摩擦力做的功。
因此,有用功的大小为:
![]()
其中f为物体所受到的阻力,s物为物体在水平方向上移动的距离。
可以看得出来,当滑轮组以水平方式使用时,有用功与物体重力的大小无关。
如图11-3-4所示,我们将货物通过斜面推上车,在这个过程中,斜面的作用是什么呢?
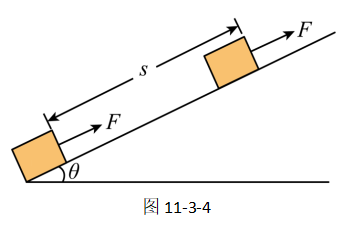
显然,此斜面的作用是为了将重物提升到某个高度上。
所以,斜面的有用功与竖直吊挂的滑轮组的有用功是一样的——重物克服重力做功。
即:
![]()
通过上述的三种机械,我们不难得出这么一个规律:使用机械时,无非是提升物体沿竖直方向上升,或者拉着物体沿水平方向前进,因此,使用机械做的有用功,要么是W有用=Gh,要么是W有用=fs。
我们还可以这样认为,所谓有用功是指不使用机械时,对物体所做的功。
比如,没有竖直滑轮组或斜面时,对物体所做的功与物体克服自身重力做的功是相等的。
使用机械时的额外功
由于滑轮组有两种使用方法,分别是竖直方式(如图11-3-2所示)、水平方式(如图11-3-3所示),对于这两种不同的使用方式,不但它们的有用功不同,额外功也是不同的。
(1)竖直滑轮组的额外功:
对于竖直滑轮组,要做的额外功是由动滑轮的自重、绕在滑轮上的绳重以及跟滑轮有关的摩擦造成的,公式可写成
![]()
一般地,最主要的额外功来自动滑轮的自重,所以,当我们忽略绳重与摩擦的影响时,竖直滑轮组的额外功只来自动滑轮的自重,则公式可变为
![]()
其中G动是指动滑轮的自重,h为动滑轮上升的高度(h也是物体上升的高度,这是因为动滑轮与物体的上升是同步的)。
需要强调的是,额外功与定滑轮的重力无关。
(2)水平滑轮组的额外功:
对于水平滑轮组,额外功主要是来自绕在滑轮上的绳重以及跟滑轮有关的摩擦造成的。
(3)斜面的额外功:
如果有斜面的表面是粗糙的,物体在沿斜面向上运动过程中克服斜面摩擦做的功,就是额外功了,公式可写成:
![]()
其中,f表示物体在斜面滑动时所受到的摩擦力,s表示斜面的长度。
斜面的额外功与摩擦力有关,水平滑轮组的有用功也与摩擦力有关。这说明,我们不能依据物体克服摩擦力做功,就断定物体一定在做额外功。
区分有用功和额外功,最根本的技巧是:假定没有机械,为完成指定目标时该物体克服某个力做的功就是有用功。
使用机械时的总功
无论是哪种机械,总功总是有用功与额外功之和。
![]()
对具体的某种机械,总功的求法还是存在一些差别。
对于滑轮组,无论是竖直滑轮组,还是水平滑轮组,都是在滑轮的绳子自由端施加一个拉力的作用,如图11-3-5所示。也就是说,我们施加的拉力并没有直接作用在物体上,而是作用在机械上(滑轮的绳子自由端上),再通过机械对物体做功。
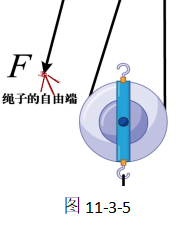
这就意味着,我们施加的拉力,不但要提升物体(做有用功),还要克服机械的摩擦等其他因素(做额外功)。
因此,两种方式的滑轮组的总功都是拉力F与拉力方向上通过的距离s的乘积,公式可表示为
![]()
其中F为作用在绕在滑轮组上的绳子自由端上的拉力,s为绳子末端沿着拉力F方向上通过的一段距离。
对于斜面,沿斜面向上推动物体上升到指定高度的过程中,不但要提升物体(做有用功),还要克服机械的摩擦等其他因素(做额外功)。
所以,推力做的功是总功,总功等于推力F与物体在斜面上通过的一段距离s的乘积,公式可表示为
![]()
其中F为作用在物体上推力,s为物体沿着推力F方向上通过的一段距离。
需要注意的是,由于物体一般都是由斜面的底部被推至斜面的顶端,所以物体被推动的距离与斜面的长度s相同的。
有关滑轮组的有用功、额外功、总功的计算
例题 ,如图11-3-6所示,工人利用滑轮组将沙子从地面提升到距地面6m高的三楼,沙子的重量为500N,动滑轮的重量为100N,工人匀速拉绳子的力为300N,忽略摩擦、绳重、桶重。
求:(1)工人做的有用功;(2)工人做的额外功;(3)工人做的总功。

【分析】求有用功时,我们不妨假定没有滑轮组时,物体上升时需要克服物重做的功;求额外功时,要区分好是题目中的情境是半理想(只忽略摩擦、桶重和绳重,没有忽略动滑轮重),还是真实情境(摩擦、绳重、动滑轮重和桶重都不能忽略)。求总功的方法有两种:一是总功等于有用功与额外功的和;二是总功等于拉力与拉力(或绳子自由端)通过的距离的乘积。
解:(1)工人做的有用功
![]()
(2)工人做的额外功
![]()
(3)工人做的总功
方法一:
![]()
方法二:
![]()
答:(1)工人做的有用国3000J;(2)工人做的额外功为600J。(3)工人做的总功为3600J。
题目中第(3)问的答案是通过两种方法求解出来的,这说明,拉力做的功就是总功。
有关斜面的有用功、额外功、总功的计算
例题,如图11-3-7所示,工人借助斜面,在100N的推力下将重400N的物体由底部推至顶部,斜面长5m,高为1m。
求:(1)工人做的有用功;(2)工人做的总功;(3)工人做的额外功;(4)物体受到斜面的摩擦力。
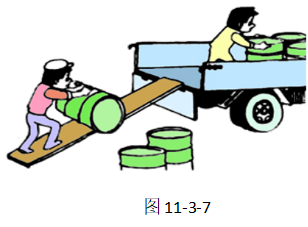
【分析】要算有用功大小,我们可假定不使用斜面时,把货物搬上货车时做的功,显然,有用功等于物体克服物重做的功;总功是推力做的功。欲求解物体在斜面上滑行的摩擦力,则需先求解额外功。由于题目没有告之摩擦力的大小,额外功的求解不能通过公式W额=fs来解答了。但可以通过总功减去有用功的方法来求解额外功。
解:
(1)工人做的有用功
![]()
(2)工人做的总功
![]()
(3)工人做的额外功
![]()
(4)物体受到斜面的摩擦力
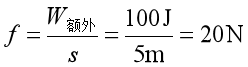
答:(1)工人做的有用功400J;(2)工人做的总功500J;(3)工人做的额外功100J;(4)物体受到斜面的摩擦力20N。
通过这个题目,我们要意识到:要求出物体在斜面上受到的摩擦力,往往先要求出斜面的额外功。
什么是机械效率
有两台塔吊正在忙着提升一些货物,如图11-3-8所示。

当两台塔吊消耗相同的电能,有一台提升的货物更多一些,这说明了什么?
这说明,提升更多货物的塔吊做的有用功更多,或者说,做的额外功更少。
在生产和生活中,我们当然都希望机械做的有用功越多越好(总功一定时),或者说,机械做的额外功越少越好(总功一定时)。如果机械具有这种性质,说明这种机械具有节省能源的优点。
物理学上,将有用功与总功的比值叫做机械效率,用η表示,η读作“eta”。公式表示为
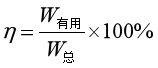
需要强调的是,“总功一定,有用功更多”其实是指有用功占总功的比例大。“总功一定,额外功少”其实指的是额外功占总功的比例小。
η一般用百分数表示,没有单位。
因此,机械效率η的大小能直观地反映出机械性能的好坏——节省能源的性能。机械效率η越大,意味着该机械的更节省能源。比如汽车,如果汽车的效率高,则意味着这样的汽车更省油。
需要强调的是,在真实情境中,任何机械都做额外功,也就是说,有用功总是比总功小,所以,机械效率不可能大于1,只会小于1。除非在理想情况下,机械的机械效率才可能等于1。
如果某起重机的机械效率是60%,它表示什么意思?
这说明使用起重机提升重物时,有用功在总功中占有60%,另外的40%是额外功占总功的比例。
有关机械效率的计算
例题 ,如图11-3-9,某起重机将重6000N的物体上升了5m,动滑轮重400N,绳重和摩擦忽略不计,求:

(1)起重机做重物做的有用功是多少?
(2)起重机做的额外功是多少?
(3)起重机做的总功是多少?
(4)起重机的机械效率是多少?
(5)当起重机提升的重物变为7600N时,它的机械效率又是多少?
【分析】本题的额外功只来自克服动滑轮自重而做的功;从题目看,总功的求解可能过有用功和额外功之和来求解。
解:
(1)起重机做重物做的有用功
![]()
(2)起重机做的额外功
![]()
(3)起重机做的总功
![]()
(4)起重机的机械效率
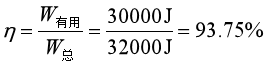
(5)若物重G2=7600N时,则此时的机械效率
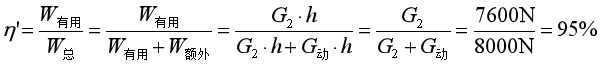
答:(1)起重机做重物做的有用功是30000J,(2)起重机做的额外功是2000J,(3)起重机做的总功是32000J,(4)起重机的机械效率是93.75%,(5)当起重机提升的重物变为7600N时,它的机械效率又是95%。
有关竖直滑轮组机械效率的其他推导公式
(1)从上面的例题,我们发现,当忽略绳重和摩擦时,机械效率还可以通过物重和动滑轮重力求出,求解表达式如下:
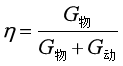
(2)针对竖直滑轮组的机械效率,我们利用s=nh的关系,还有其他的推导公式:
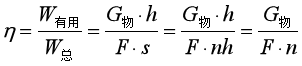
从上面的推导式,我们可以看出,机械效率通过物重、拉力和绳子的股数求出,最终的表达式如下:
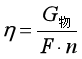
需要强调的是,第(1)个推导式具有物理意义,因为它可以让我们看出,机械效率是由物重和动滑轮重决定的(绳重和摩擦忽略不计);但第(2)个推导式却没有物理意义,只有计算意义,也就是说,第(2)个推导式不能说明机械效率与拉力、绳子股数有关。
竖直滑轮组的机械效率的影响因素
从图11-3-7的例题的第(4)问答案和第(5)问答案的比较,我们发现,竖直滑轮组的机械效率与物重有关。即物重越大,机械效率越大。
但竖直滑轮组的机械效果不仅仅是与物重有关,若保持物重不变时,减少动滑轮重、绳重、绳与滑轮的摩擦,可以减小额外功占总功的比例,也可以提高竖直滑轮组的机械效率。
因此,影响竖直滑轮组的机械效率的影响因素有:物重、动滑轮重、绳重、绳与滑轮的摩擦等四个因素。
与机械效率无关的因素
前面我们说了,竖直滑轮组的机械效率与绳子股数无关?
可能有人会困惑,第(2)推导式明明显示机械效率与绳子股数啊,因为只改变滑轮组的绳子的绕法(即改变滑轮组的绳子的股数),一定会改变了拉力的大小,总功看似也会发生改变。真的是这样的吗?
例题,如图11-3-10所示,有甲乙两个滑轮组,分别提升10N的钩码,提升的高度均为1m,动滑轮重2N,忽略绳重和摩擦。试求两个滑轮组分别做的总功。
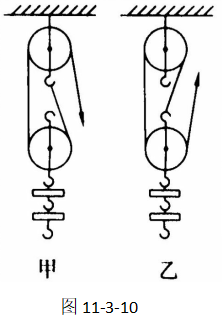
解:【分析】两个滑轮组提升的重物的重力是一样的,提升的高度也是一样的,所以,两个滑轮组做的有用功是一样的。
甲滑轮组的拉力
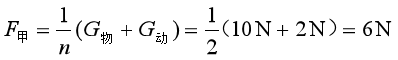
甲滑轮组的绳端移动的距离
![]()
则甲滑轮组的拉力做的总功
![]()
乙滑轮组的拉力
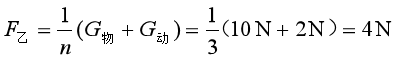
乙滑轮组的绳端移动的距离
![]()
则乙滑轮组的拉力做的总功
![]()
由数据可知
![]()
答:两个滑轮组分别做的总功是一样大的。
从这个题目可以看出,改变绳子股数,虽改变了拉力,但拉力变小时,拉力移动的距离却增大,最终造成拉力做的功并没有发生改变。因此,只有绳子股数的变化,并不能改变滑轮组的机械效率。
只是改变匀速上升的速度大小,也不能改变滑轮组的机械效率。比如物体以1m/s的速度匀速上升变为以2m/s的速度匀速上升时,滑轮组的机械效率也不会发生改变的,但拉力做功的功率(也称总功率)和物体克服物体重力做功的功率(也称有用功率)都会变大。
这个事实也说明了,虽然功率与机械效率都能反映机械的性能好坏,但功率反映了做功的快慢性能,机械效率反映了做功的节能性能。
机械效率与功率是相互独立的、互不影响的物理量,两者之间不存在必然关系。也就是说,功率大的机械,它的机械效率可能小,也可能大。
水平滑轮组的机械效率的影响因素
对于水平滑轮组,物体克服水平地面摩擦所做的功是有用功,而克服绳与滑轮的摩擦做的功是额外功。所以,减小绳与滑轮的摩擦也可以增大机械效率。
水平滑轮组的机械效率的公式如下:
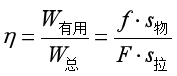
其中s物是指物体在水平地面滑行的距离,s拉是指绳子自由端在拉力的作用下沿拉力方向通过的距离。滑轮组虽然是水平方向的,但s拉与s物之间存在固定的比例关系,即
![]()
其中,n是滑轮组的绳子的股数。所以,求解水平滑轮组的机械效率的公式可推导为
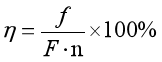
竖直滑轮组与水平滑轮组的机械效率辨析
我们将竖直滑轮组与水平滑轮组进行比较,我们不难发现以下异同点:
斜面的机械效率的影响因素
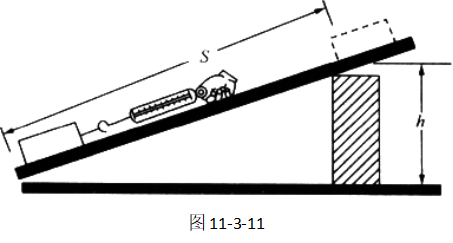
对于斜面,如图11-3-11所示,物体克服物体重力上升时所做的功是有用功。
所以,增加物重是可以提高斜面的机械效率的。
斜面的额外功是指克服斜面的摩擦力做的功,
很显然,在保持物重不变的情况下,增加斜面的倾斜程度(或增大倾角)和减小斜面的粗糙程度可以大大减小斜面对物体的摩擦力,从而可以提高机械效率。
所以,提高斜面的机械效率的方法有:
1、增加物重;
2、增加斜面的倾斜程度(即增大斜面的倾角);
3、减小斜面的粗糙程度。
【本节课学到的内容】
1、有用功、额外功、总功的定义
我们需要的、有价值的功,叫做有用功,记作W有用;
像这类不需要,但又不得不做的功,我们称为额外功,记作W额外。
有用功和额外功的总和叫做总功,用W总表示。
2、机械效率的定义
物理学上,将有用功与总功的比值叫做机械效率,用η表示。
3、机械效率的影响因素
(1)竖直滑轮组:物重、动滑轮重、绳重、绳与滑轮的摩擦。
(2)水平滑轮组:物体与水平地面的摩擦、绳与滑轮的摩擦。
(3)斜面:物重、斜面的倾斜程度、斜面的粗糙程度。
【自我检测与巩固】
1、下列有关机械做功、功率、机械效率的说法,正确的是 ( )
A.机械效率越高的机械,功率越大。
B.做功越多的机械,功率越大。
C.做有用功越多的机械,机械效率越高。
D.功率越大的机械,做功越快。
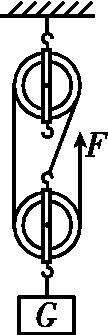
2、如图所示,用滑轮组将重为540 N的重物匀速提升2 m,所用拉力F 为200 N,
求:(1)该滑轮组的机械效率为多少?
(2)如果要提高滑轮组的机械效率,你的做法是什么?(答出一条即可)
3、如图所示的滑轮组拉动重300 N的箱子,以0.2 m/s的速度在水平地面上做匀速直线运动,箱子与地面间的摩擦力为自身所受重力的0.2倍,滑轮组的机械效率为75%,则
(1)拉力是多少?
(2)拉力做功的功率是多少?
Was this helpful?
1 / 0