14.2 欧姆定律
【与教材不同之处】
更详细描述电流与电压、电阻的实验探究过程;更详细描述对欧姆定律的公式的理解;更详细描述通过欧姆定律推导串、并联电路总电阻;更详细描述欧姆定律在串、并联电路中的应用。
电流与电压、电阻
电路两端有电压时,电路中才会有电流。而且通过实验,我们发现,当电路两端的电压越大,则电路中的电流也会越大。
通过实验,我们还发现,当电路中的某个电阻的阻值变大时,电路中的电流会变小。
这说明,电压和电阻都是影响电路中的电流大小的因素。
那么,电流与电压是否成正比,与电阻是否成反比?
探究电流与电压的定量关系
由于电流的影响因素有两个,所以,本实验我们要采用控制变量法。
(1)探究电流与电压关系时,电阻保持不变;
(2)探究电流与电阻关系时,电压保持不变。
所以,本实验分两个部分进行。
我们首先来探究电流与电压的关系。
根据控制变量法,本次实验需要保持不变的量是电阻,也就是说,实验中的导体必须是一个电阻不变的导体,比如定值电阻。
本次实验需要改变的量是电压,在本次实验中我们采用改变电池节数的方式来改变导体两端的电压。
电路的实物图和电路图如14-2-1所示。
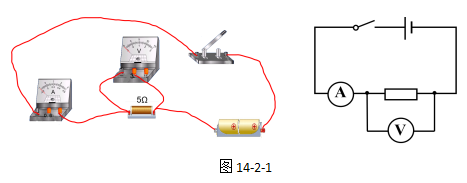 其中电流表用来测量通过定值电阻的电流,电压表用来测量定值电阻两端的电压,导体是一个已知阻值为5Ω的定值电阻。
其中电流表用来测量通过定值电阻的电流,电压表用来测量定值电阻两端的电压,导体是一个已知阻值为5Ω的定值电阻。
实验步骤如下:
(1)选择5Ω的定值电阻接入电路中,闭合开关后,记录电压与电流的示数;
(2)更换电池的节数,再记录电压与电流的示数(注意,更换电池节数前要断开开关)。
实验的数据记录如表1。

通过对实验数据的分析,我们发现,当导体两端的电压增大一倍,通过导体的电流也增大一倍。
这的确说明,当导体的电阻一定时,通过导体的电流与导体两端的电压是成正比的。
此结论也可简洁地说成:电阻一定,电流与电压成正比。
探究电流与电压定量关系过程中反思与评估
有时,我们在实验过程中得到的实验数据如表2:
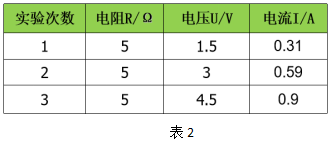
可以有两种方法来解决。分析表格的数据,当电压成倍数增加时,电流表的示数好像并没有随着成倍数增加,那么,根据这样的数据我们如何得出科学的结论呢?
方法一:增加实验的次数。
实验次数越多,越有助于发现数据之间的规律。
由于改变电池的节数不可能无限制地增加的,如果这样做,通过导体的电流值会超过电流表的最大量程。也就是说,通过改变电池节数来改变导体两端的电压,进而实现多次实验的方法是存在缺陷的。
所以,为了使实验次数的增加不受限制,在电路中串联一个滑动变阻器不失是一个好的选择。新的电路图如14-2-2所示:
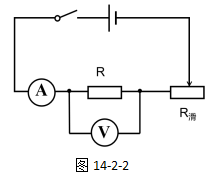
有了滑动变阻器,我们只要稍稍移动滑动变阻器的滑片,定值电阻两端的电压就可以发生改变,从而就可以进行一次新的实验,操作也变得非常方便。
虽然此实验中滑动变阻器的作用虽然不是必需的,但使用它的好处很明显:
(1)保护电路;
(2)非常方便地多次改变导体两端的电压;
(3)还可以让导体两端的电压成倍数变化,以便于我们发现规律。
方法二:绘制图像
如果进行了多次实验后,为了快捷地形象地看到数据之间的规律,我们可以把实验数据标注在电压-电流坐标图中(电压为横轴、电流为纵轴),然后画一条最光滑的曲线尽可能地经过所有的点。
比如,根据表2的数据作图后,我们很快地会发现,有一条经过原点的斜的直线能基本上经过了所有的点,如图14-2-3所示。
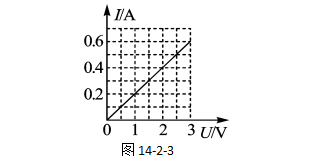
斜的直线说明了当电压成倍数增加时,电流也在成倍数增加的事实。或者也可以说明,电压与电流的比值是一个固定值。
总之,由图像我们可以得出:电阻一定时,电流与电压是成正比的定量关系。
探究电流与电阻的定量关系
根据控制变量法,本次探究电流与电阻关系的实验需要保持不变的量是电压,也就是说,实验中的导体两端的电压必须保持不变。
本次实验需要改变的量是电阻,比如,用5Ω的定值电阻进行实验后,断开开关后,取下5Ω的定值电阻,换成10Ω的定值电阻,再进行新的实验。
实验步骤如下:
(1)选择5Ω的定值电阻接入电路中,闭合开关后,记录电压表与电流表的示数;
(2)断开开关,取下5Ω的定值电阻,换上10Ω的定值电阻,再记录电压表与电流表的示数。
需要注意的是,当换上10Ω的定值电阻,闭合开关后,发现定值电阻两端的电压发生变化,可是,本次实验的前提条件是导体两端的电压必须保持不变。
所以,既要改变导体的电阻,又要保持导体两端的电压不变,这个问题如何解决?
解决方法是:串联一个滑动变阻器。
此时实验的实物图和电路图如14-2-4所示。
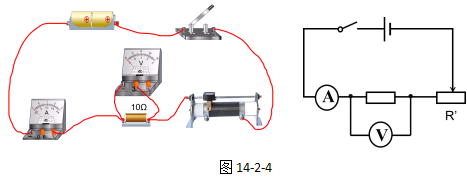
则实验步骤(2)应当描述为:断开开关,取下5Ω的定值电阻,换上10Ω的定值电阻,通过移动滑动变阻器的滑片,使电压表的示数与步骤(1)中的电压表的示数相同,再记录此是电流表的示数。
继续进行更换定值电阻再重复步骤(2)进行多次实验,实验的数据记录如表3。
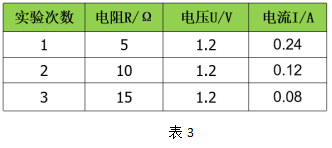
通过对实验数据的分析,我们发现,当导体的电阻增大一倍,通过导体的电流却减小一倍。这的确说明,当导体两端的电压一定时,通过导体的电流与导体的电阻成反比。
此结论也可简洁地说成:电压一定,电流与电阻成反比。
保持电压一定,滑动变阻器如何调节
在此实验过程中,定值电阻由5Ω变为10Ω时,滑动变阻器的滑片将如何移动?
通过实验,我们会得到一条规律:定值电阻替换为更大的阻值时,为了保持定值电阻两端的电压不变,滑动变阻器的滑片应当向阻值更大的方向移动。
此操作方法的口诀为:电压不变,同大同小。口诀中“同大同小”是指定值电阻变大,则滑动变阻器的阻值也要变大。
现在我们可以对滑动变阻器的作用做一个总结:
(1)在探究电流与电压的关系是,滑动变阻器的作用是改变导体两端的电压;
(2)在探究电流与电阻的关系是,滑动变阻器的作用是保持导体两端的电压不变。
也就是说,当实验目的不同时,滑动变阻器的作用是相反的。
电流与电阻的图像
在探究电流与电压时,U-V的图像是一条倾斜的直线。从而我们得到了电流与电压成正比的规律。
类似的,我们将实验中电流与电阻的数据标注在R-I的图像中,当把这些点连接起来,发现这不再是一条直线,而是一条光滑的曲线,如图14-2-5所示。
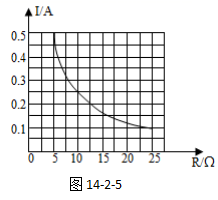
在这条光滑的曲线上的每个点的横坐标的大小与纵坐标的大小的乘积都极为接近一个定值,也就是说,这是一条双曲线。从数学角度分析,我们断定,电流与电阻是成反比的。
欧姆定律的内容
通过上述的实验,我们得到结论如下:
电阻一定,电流与电压成正比。
电压一定,电流与电阻成反比。
这两句话,这就是欧姆定律的全部内容。
因此,欧姆定律其实是描述电流与电压、电阻之间定量关系的一个规律。
由于电流与电压成正比,与电阻成反比,我们可以得到这么一个公式:
![]()
公式中单位要统一,分别用A、V、Ω;
这个公式是具有物理意义的,因为它很好地体现了电流与电压成正比,与电阻成反比的定量关系。
欧姆定律的公式可变形为:
![]()
此公式用于已知的电压值和电流值求解某个导体的阻值。
需要注意的是,虽然电阻可以由电压与电流的比值求解出来,但电阻与电压、电流是无关的,因为电阻是导体的属性,电阻只与导体的长度、横截面积、材料种类以及温度有关。
此公式只是用来计算电阻大小的计算式,并不能反映电阻的影响因素是什么,因此,此公式不具有物理意义。
欧姆定律的公式还可变形为:
![]()
此公式用于已知的电流值和某个导体的电阻值时求解出这个导体两端的电压。
利用欧姆定律的公式来解题
例题:某实验中测得一个未知电阻的电压为4.8V,流过的电流是320mA,求该电阻的阻值。
【分析】此题要注意的地方是要将电流320mA换算成0.32A后,才能代入公式中计算。
解:
I=320mA=0.32A
![]()
答:电阻的阻值为15Ω。
串联电路总电阻的推导
如图14-2-6,已知串联电路中的两个电阻的阻值分别为R1、R2,电源电压为U,闭合开关S后,电路电流为I,试推导电路的总电阻是多少?
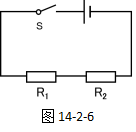
以及串联电路的电压、电流的特点:U=U1+U2、I=I1=I2,我们可以进行如下的推导过程:根据欧姆定律的变形公式
![]()
因此,我们得到串联电路的总电阻与各电阻的关系——串联电路的总电阻等于各部分电阻之和,公式如下:
![]()
这个公式说明,导体串联后的总电阻比任何一个单独导体电阻R1或R2都要大,而且是两个电阻值之和。
![]()
为什么两个导体串联后总电阻会变大呢?
因为导体串联相当于使导体的长度变大了。
并联电路总电阻的推导
如图14-2-7,已知并联电路中的两个电阻的阻值分别为R1、R2,电源电压为U,闭合开关S后,干路中的电流为I,试推导电路的总电阻是多少?
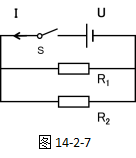
根据欧姆定律的变形公式
![]()
以及并联电路的电压、电流的特点:U=U1=U2、I=I1+I2,我们可以进行如下的推导过程:
因此,我们得到并联电路中总电阻与各电阻的关系:
![]()
这个公式如果取它的倒数,还有一种写法:
![]()
于是,我们得到了并联电路的总电阻与各电阻的关系——并联电路的总电阻的倒数等于各支路部分电阻的倒数之和。
这个公式说明,导体并联后的总电阻比任何一个单独导体电阻R1或R2都要小。
为什么两个导体并联后总电阻反而变小呢?
因为导体并联相当于使导体的横截面积变大。
欧姆定律在串联电路中计算应用
例题:如图14-2-8所示,电源电压为3 V,闭合开关S后,电流表示数为0.2 A,R1两端的电压为1 V,则R1、R2的阻值各是多少。
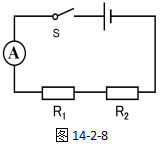
【分析】当电路中有两个用电器时,无论是串联还是并联,利用欧姆定律计算时,要遵循“同一性”原则,比如,R1的阻值大小只能是用R1两端的电压和通过R1的电流来求解。
因此,要想利用欧姆定律来求出R1、R2的阻值,就必须先求出它们各自的电压与电流。
本题中,电流表的示数测量的是电路电流,也叫总电流。由于是串联,R1、R2的电流与总电流是相等的,R1、R2的电压之和等于总电压。因此,根据串联电路的电压、电流规律,我们是可以分别求出R1、R2的电压和电流的。
我们的计算过程的表达式如下:
解:
因为串联,所以
![]()
根据欧姆定律,得
![]()
因为串联,所以
![]()
根据欧姆定律,得
![]()
答:R1的电阻为5Ω,R2的电阻为10Ω。
需要强调的是,求R2阻值的方法还有另外一种——先通过欧姆定律求出电路的总电阻,再根据串联电路的电阻特点求解出R2的大小,具体的解题过程如下:
根据欧姆定律,得到总电阻
![]()
因为串联,所以
![]()
通过这道题,我们发现,如果用电器有两个(用电器可以是电阻或灯泡)串联在一起时,有关电路的计算总共涉及到9个物理量,它们之间的关系见表4:
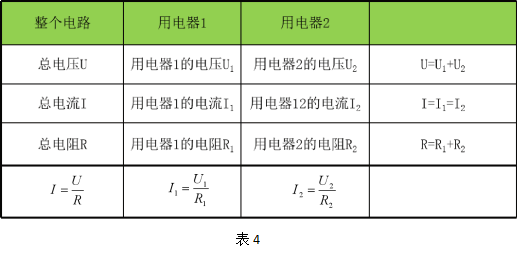 从上表可以看出,电流、电压、电阻之间存在两个维度的关系,分别是欧姆定律和串联电路的特点,因此,一般只要知道其中3个物理量,我们就可以求解出其他6个物理量。
从上表可以看出,电流、电压、电阻之间存在两个维度的关系,分别是欧姆定律和串联电路的特点,因此,一般只要知道其中3个物理量,我们就可以求解出其他6个物理量。
比如上题,我们知道的物理量是:总电压(又称电源电压)U=3V;总电流(又称电路电流)I=0.2A;电阻R1的电压U1=1V。
如果把已知条件填入上表中,我将很容易,又清晰地求解出其他的物理量,见表5。

这种求解电流、电压、电阻的方法我们不妨称之为“九宫图”法。
欧姆定律在并联电路中计算应用
例题,如图14-2-13所示,已知R2=15Ω,闭合开关S后,电流表A1,A2的示数分别为0.5A,0.2A,则通过R1的电流是多少?电源电压是多少?
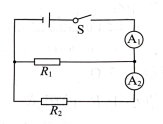
【分析】本题中,不仅有两个定值电阻,还有多个电流表,所以,不但要判断两个电阻的连接方式,还要判断两个电流表各自的测量对象是谁。
通过“小拆法”,我们知道此电路是并联;通过“拆表法”,我们知道电流表A1的测量对象是定值电路R1和R2的总电流;电流表A2测量对象是定值电路R2的电流。
根据已知条件求解出未知物理量,可采用“九宫图”,我们把已知条件填入九宫表中,我们很快就可以求出未知的量,见表6。

有了解题的思路,即有了方向,下笔计算时就可以做到“下笔如有神”之感了。
解:电流表的测量对象的电流大小如下:
![]()
此电路是并联电路,所以过R1的电流为
![]()
此电路是并联电路,所以电源电压为
![]()
答:通过R1的电流是0.3A,电源电压是3V。
欧姆规律发现的由来
最初,意大利科学家伏特发明电池后,德国科学家塞贝克也发明了一种新电池:温差电池。温差电池的优点是当电源两极的温差恒定,则产生的电流稳定。
同期,法国数学家、物理学家傅里叶提出了有关热传导的傅里叶定律。其文字表述是:在导热现象中,单位时间内通过给定截面的热量,跟垂直于该截面方向上的温度变化率成正比……。
德国的一位中学教师欧姆受到傅里叶热传导理论的启发,他把电压比作温度差,将电流比作单位时间内传递的热量,用塞贝克发明的温差电池来对电流做出类似的分析。
为了测量电流的大小,手巧的欧姆发明了一种电流扭秤(即电流越大,挂在扭丝下的指针偏转的角度越大)。这个电流扭秤其实就是当今电流表的雏形。
1826年,欧姆正式提出欧姆定律:X=a/L。该公式是欧姆定律的最初形式,X代表电流,a代表电压,L代表电阻。
当时德国科学界不承认欧姆的发现,认为这个定律太简单,不足为信。但是英国科学家波利特在实验中多次引用欧姆定律,都能得出准确的结果,于是欧姆定律最终得到了认可。
【本节我们学到的内容】
1、欧姆定律的内容是什么
电阻一定,电流与电压成正比。
电压一定,电流与电阻成反比。
2、欧姆定律的公式
![]()
3、在探究欧姆定律的实验中,滑动变阻器的作用是什么
由于此实验分两个部分,实验目的不同时,滑动变阻器的作用是不同的。
(1)在探究电流与电压的关系是,滑动变阻器的作用是改变导体两端的电压;
(2)在探究电流与电阻的关系是,滑动变阻器的作用是保持导体两端的电压不变。
4、串联电路的总电阻的推导
![]()
5、并联电路的总电阻的推导
![]()
6、欧姆定律在串、并联电路中解题技巧
可采用“九宫图”法。
7、欧姆定律在多电表的多用电器的电路中的解题步骤
步骤如下:
(1)判断电路的连接方式;
(2)判断电表的测量对象;
(3)使用九宫图法求解出未知物理量。
【自我检测与巩固】
1、如图所示是探究“电流跟电压关系”的实验,下列说法不正确的是( )
A、探究电流跟电压的关系时,需要控制导体的电阻一定
B、滑动变阻器可以起到改变定值电阻两端电压的作用
C、实验的结论是:电流跟电压成反比
D、多次实验是为了得到电流跟电压之间的定量关系
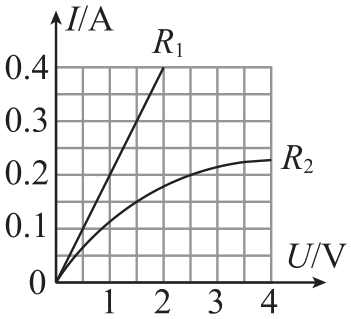
2、小明在研究通过导体的电流与其两端电压的关系时,根据测量数据绘制出如图所示的I−U 图像。下列判断正确的是( )
A、通过R_1 的电流与其两端所加电压不成正比
B、通过R_2 的电流与其两端所加电压成正比
C、将它们串联接到电路中时,通过R_1 的电流较大
D、将它们并联接到电压为1.5 V 的电源两端,通过干路的电流是0.45 A
3、如图所示,电路中定值电阻R1阻值为10Ω ,电源电压不变。只闭合S1,电流表的示数为0.3A;S1、S2 均闭合,电流表的示数为0.5A,此时通过R1 的电流为多少安?R2的阻值为多少欧姆?
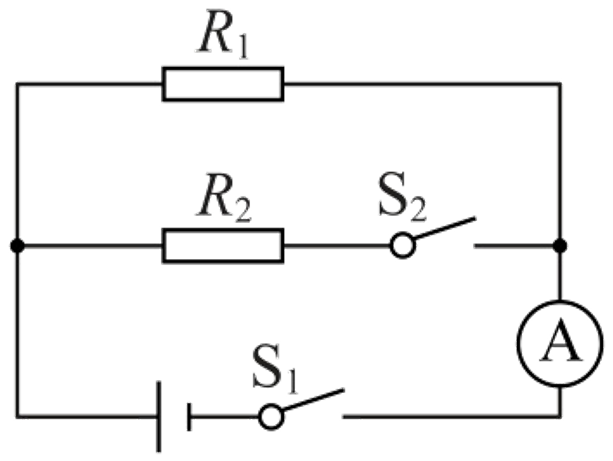
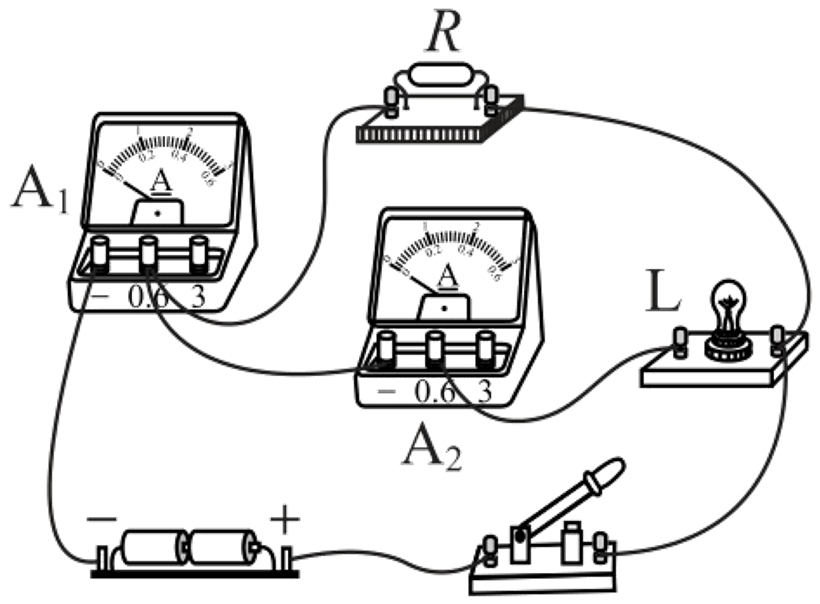
4、如图所示电路,在闭合开关后,电流表A1的示数为0.5A,电流表的示数为0.1A,当灯正常工作时的电阻是10Ω,则定值电阻的阻值是多少?电源电压是多少?
Was this helpful?
1 / 0