14.3 欧姆定律的应用
【与教材不同之处】
更详细描述测量小灯泡电阻实验的过程和故障分析，更详细描述特殊方法测量未知电阻的方法；更详细描述串联分压定律和并联分流定律；更详细描述动态电路的定性分析与定量计算；更详细描述滑动变阻器的极值问题。
测量小灯泡的电阻
我们如何测量小灯泡发光时的电阻呢？如图14-3-1所示。
欧姆定律的公式有一个变形公式为：
根据这个变形公式可以帮助我们测量出小灯泡发光时的电阻——只要测量出小灯泡两端的电压和通过小灯泡的电流，通过两者的比值便可测算出小灯泡的阻值，这种方法称为“伏安法”测电阻。
因此，本实验需要的仪器除了灯泡，电源、开关等，还需要电压表、电流表。
需要注意的是，本实验最好再加一个滑动变阻器。
之所以加一个滑动变阻器，是因为通过滑动变阻器的滑片的移动，便可以非常方便地改变灯泡的亮度，读出此时灯泡两端的电压和通过灯泡的电流，从而可以测量出灯泡不同亮度下的灯泡的电阻。
实验步骤如下：根据上述的实验器材，测量灯泡电阻的实验器材连成的实物图和电路图如14-3-2所示。
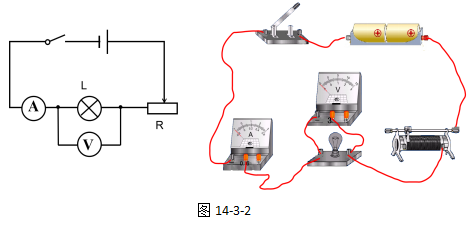
（1）按图组成电路，闭合开关，移动滑片，使小灯泡发光较暗，读出此时的电压表和电流表的示数。（注：闭合开关前，滑动变阻器的滑片位于阻值最大处，此为了保护电路）
（2）移动滑动变阻器的滑片，使小灯泡正常发光，读出此时的电压表与电流的示数。
（3）移动滑动变阻器的滑片，使小灯泡发光明亮，读出此时的电压表与电流的示数。
将上述数据填入表中，见表1。
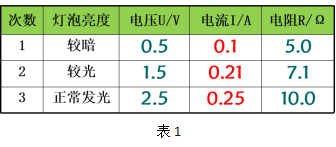
通过分析表格中的数据，我们发现灯泡的电阻是变化的。
如果把表格中的数据U-I坐标图表示出来，我们将看到一条弯曲的线，如图14-3-3所示。
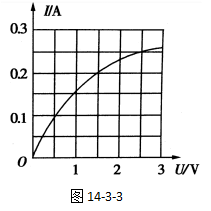
灯泡的电阻为什么会发生改变呢？
有些同学可能会认为，灯泡电阻发生改变的原因是灯泡的两端的电压发生了变化，因为表格中，当灯泡两端的电压越大，灯泡的电阻也会越大。
也有些同学还认为，灯泡电阻发生改变的原因是通过灯泡的电流发生了变化，因为表格中，当通过灯泡的电流越大，灯泡的电阻也会越大。
在本章的第一节，我们就探究过导体电阻的影响因素，我们得到的结论是：导体电阻与导体的材料、长度、横截面积以及温度有关，与电压、电流无关。
因为有这么一个事实，当电压和电流变小为0，灯泡的电阻却不为0，也就是说，没有电压、电流，灯泡的电阻仍然存在。这就说明了，灯泡的电阻与电压、电流是无关的。
原来，当电压、电流增大时，灯泡越亮，则意味着灯丝的温度将会更高，因此，灯泡的电阻之所以发生变化，是因为灯丝的温度不同造成的。于是，我们得到的结论是：灯丝的电阻随温度的升高而增大。
需要强调的是，灯泡的电阻不同，不是因为误差原因而造成的，对不同的电阻值求平均值是没有意义的。所以，此实验进行多次实验，是为了得到一个更具有普遍性的结论——灯丝的电阻因温度不同而改变。
如果我们的实验对象是阻值未知的定值电阻，即可忽略温度对定值电阻的影响，如果每次实验时的定值电阻的阻值仍略微不同，这种电阻不同的原因只能是误差造成的，所以，此时对不同的阻值需要采用求平均值，以减小误差。
电路故障分析
在测量小灯泡的电阻的实验中，常常会出现如下故障情形：
（1）电流表无示数，电压表有示数（接近电源电压）
无论是测量小灯泡的电阻，还是测量未知定值电阻的阻值，电路的连接方式都属于串联电路，因此，电流表无示数，则意味着电路中某处断路。
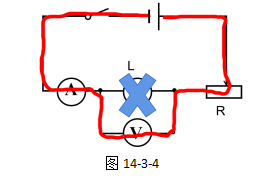
如果电压表有示数，则意味着电压表与电源之间形成了闭合回路， 如图14-3-4所示的电路中的红线部分的电路。
所以，要同时出现电流表无示数、电压表有示数的现象，则电路中只能是灯泡处断路，如图14-3-4所示。
（2）电流表有示数，电压表无示数。
电流表有示数，则电流表与电源之间形成了闭合回路，是通路。如果电压表是正常的，电压表的接线柱的接线正常，也就是说，电压与电源之间也是可以形成闭合回路的，但电压表的示数仍为零，只有一种可能——电压表的测量对象灯泡处短路（比如装有灯泡的灯座的内部有导线直接相连），从而造成电压表也被短路了，灯泡此时也不会发光。
如何只使用一个电流表测量电阻——安阻法
有时，身边只有一个电流表，是否可以测出未知阻值的定值电阻器（也称为待测电阻，一般用Rx表示）的电阻呢？
显然，只有一个电流表，只能测出通过待测电阻的电流。根据伏安法测电阻的方法，除了要知道通过待测电阻的电流，还要知道待测电阻两端的电压。
如何利用电流表测出电压呢？
如图14-3-5所示，我们观察到，电压表测量未知阻值的定值电阻器RX的电压时，其实是电压表与RX并联。
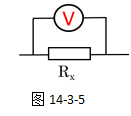
图14-3-6中的左图所示，R0是一个已知阻值的定值电阻，此时R0和 Rx是并联的，根据并联电路的电压规律，因此它们的电压是相等的，所以，如果我们有办法知道R0的电压，也就知道了Rx的电压。
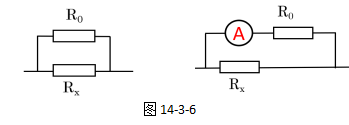
将R0与电流表串联（图14-3-6中的右图所示），则根据欧姆定律的变形公式U=IR可知，电流表的示数与R0阻值的乘积便是R0两端的电压。因此，电流表与R0组合在一起其实起到了电压表的作用，两者是等效的。
因此，我们需要两个电流表或将电流表使用两次，分别测出：
（1）通过RX的电流；
（2）通过R0的电流（此电流其实是为了间接测出Rx两端的电压）。
通过电流表测量两次不同的电流从而可测出待测电阻的阻值，这种方法称为“安阻法”。
例题1：如图14-3-7所示，某同学利用一个电流表和已知电阻R0来测量未知电阻RX的阻值的实验电路图，写出实验步骤并写出测算出Rx的表达式。
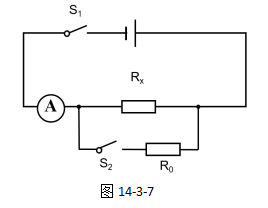
【分析】两个开关的闭合、断开情况只有两种：分别是“S1闭合，S2断开”和“S1和S2闭合”，因此实验步骤分两步。
解：实验步骤如下：
（1）当S1闭合，S2断开时，电流表测量的是通过Rx的电流，设为I1；
（2）当S1和S2闭合时，电流表测量的是R0和Rx的总电流，设为I2。
【分析】从上面两步的测量结果，好像只是测量出了Rx的电流，没有测量出R0的电流，其实，根据并联电路的电流规律，R0的电流等于这两次电流之差，即I0=I2-I1。
利用电流值I2和I1，我们可以推导出测量出RX的阻值大小的表达式，如下：
如何只使用一个电压表测量电阻——伏阻法
如果只有一个电压表，我们将如何测量待测电阻的阻值呢？
我们遇到的问题与前面是类似的，当只有一个电压表时，只能测出待测电阻两端的电压，不能直接测出待测电阻的电流。
如何测量通过待测电阻的电流呢？
方法是类似的，我们可以通过一个电压表与已知阻值的电阻进行组合，让这个组合能起到电流表的作用，如图14-3-8所示。
通过电压表测量两次不同的电压从而测出待测电阻的阻值，这种方法称为“伏阻法”。电压表的示数与已知电阻器R0的阻值的比值等于通过R0的电流，根据串联电路的电流特点，通过Rx的电流与通过R0的电流是相等的，因此，Rx的电流便可测出。
例题：如图14-3-9所示，某同学利用一个电压表和已知电阻R0来测量未知电阻RX的阻值的实验电路图，写出实验步骤并写出测算出Rx的表达式。
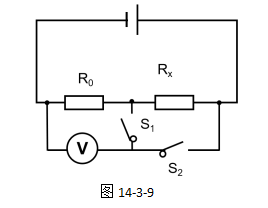
解：实验步骤如下：【分析】两个开关的闭合、断开情况只有两种：分别是“S1闭合，S2断开”和“S1断开，S2闭合”，因此实验步骤分两步。
（1）当S1闭合，S2断开时，电压表测量的是通过R0的电压，设为U1；
（2）当S1断开，S2闭合时，电压表测量的是R0和Rx的总电压，设为U2。
【分析】从上面两步的测量结果，好像只是测量出了R0的电压，没有测量出Rx的电压，其实，根据串联电路的电压规律，Rx的电流等于这两次电压之差，即UX=U2-U1。
利用电压值U2和U1，我们可以推导出测量出RX的阻值大小的表达式，如下：
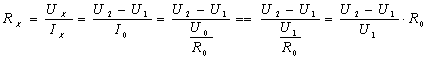
例题2：如图14-3-10所示的电路图，可以求出未知电阻Rx的阻值吗？
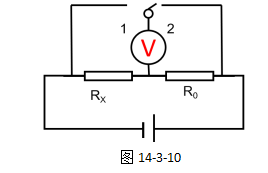
【分析】当开关接至“1”处时，电压表测量的是Rx的电压，当开关接至“2”处时，电压表测量的是R0的电压，则求出Rx电阻的表达式过程如下：
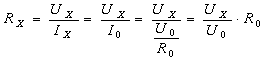
表面上看，我们是可以求出Rx的阻值的，但当开关由“1”改接至“2”处时，电压表的上面的接线柱的接线由开始接负极变为正极，也就是说，当开关由“1”改接至“2”处时，电压表的指针会反偏。因此，图14-3-8所示的电路图是不能求出未知电阻Rx的阻值的。
通过上面的例题分析，我们发现，如果想用一个电表（电流表或电压表）测出RX的阻值时，则须满足两个条件：
（1）电流表（或电压表）能使用两次，每次的测量对象是不同的（测量对象可以是已知阻值的电阻R0，也可是待测电阻RX，还可以是整个电路）；
（2）在开关闭合情况发生改变时，注意电表的接线不能出现错误。
串联分压定律的推导
例题：如图14-3-11所示，有两个电阻R1和R2，它们阻值分别是5Ω和10Ω，电源电压是3V，试求解出R1和R2的电压分别是多少？
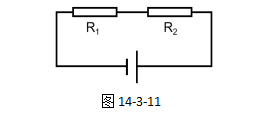【分析】由于两个电阻串联，所以它们的总电阻是各个电阻之和，则求解R1和R2的电压过程如下：
解：根据欧姆定律，电路总电流为
因此，R1和R2的电流为
根据欧姆定律，R1的电压为
根据欧姆定律，R2的电压为
通过这个例题，我们发现，R1比R2的阻值小，R1的电压也比R2的电压小。因此，我们可以得到这么一个结论：在串联电路中，电阻大的所分得的电压也大。
如果将两个电阻之比再进一步推导，推导过程如下：
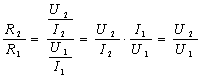
我们发现，若电阻之比等于它们电压之比，则用公式表示为
这个规律一般称之为串联分压定律。
因此，当一个定值电阻与滑动变阻器串联时，如图14-3-10所示。
若移动滑片后使滑动变阻器连入电路的阻值变大时，根据串联分压定律，滑动变阻器两端的电压将会变大，由于总电压（电源电压是一定的），则定值电阻分得电压将变小（虽然定值电阻的电阻没有变化）。
并联分流定律的推导
例题：如图14-3-13所示，有两个电阻R1和R2，它们阻值分别是5Ω和10Ω，电源电压是3V，试求解出R1和R2的电压分别是多少？
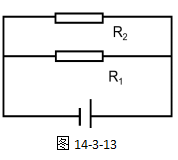
【分析】由于两个电阻并联，所以它们的电压是相等的，且都与电源电压相等，则求解R1和R2的电流过程如下：
解：R1和R2的电压为流过程如下：
因此，根据欧姆定律，R1的电流为
根据欧姆定律，R2的电流为
通过这个例题，我们发现，R1比R2的阻值小，通过R1的电流比R2的电流反而更大。因此，我们可以得到这么一个结论：在并联电路中，电阻小的通过的电流反而大。
如果将两个电阻之比再进一步推导，推导过程如下：
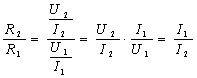
我们发现，若电阻之比等于它们电压之比，则用公式表示为
这个规律一般称之为并联分流定律。
有关动态电路的定性分析
例题：如图14-3-14所示，当滑动变阻器的滑片向右移动时，请分析电流表与电压表的示数变化。
【分析】这类判断电表示数变化的题目，我们的分析过程一般分为五步：
（1）判断用电器的连接方式；
（2）判断各电表的测量对象；
（3）分析滑动变阻器的阻值的变化情况；
（4）先分析电流表示数变化；
（5）再分析电压表示数的变化。
解：此电路中的滑动变阻器R与定值电阻R0是串联的，电流表测量对象是电路电流（总电流），电压表测量对象是R两端的电压。滑片向右移，则滑动变阻器R连入电路中的阻值在变大。
由于R变大，则电路中的总电阻也变大，根据欧姆定律I=U/R可知，当总电压U不变，总电阻变大，则电路电流（总电流）变小，所以，电流表的示数变小。
由于R变大，根据串联分压定律可知，则R两端的电压也会变大，所以，电压表的示数变大。
电路中的电流表或电压表示数会发生改变，也可能来自开关的闭合与断开，但分析过程跟上面的分析过程是一样的。
有关动态电路的定量计算
什么是动态电路？
当电路中的开关闭合与断开情况发生变化时，或连入电路中的滑动变阻器的阻值发生变化时，可能造成电路中用电器的连接方式发生变化，从而造成电路中的电流与电压也可能会发生相应的变化，这种电路称为动态电路。
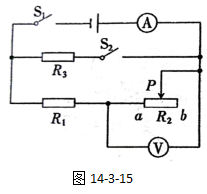
例题：如图14-3-15所示，R1=25Ω，R2为滑动变阻器，电源电压保持不变。当S1闭合，S2断开时，若滑片P在a端，则电流表示数为0.6A；若滑片P在b端，则电压表示数为10V。
求：(1）电源电压；
(2）滑动变阻器R2的最大阻值；
【分析】由于动态电路在不同的时刻有不同的电路连接方式，因此，我们首先要做的就是——将每个时刻的电路都进行分析。
需要注意的是，虽然每个时刻的电路连接方式不同，电流表和电压表的示数也可能发生变化，但在任何时刻的电路里，有两个量基本上是不变的，它们是电源电压和定值电阻的阻值，因此，我们在解题过程中要利用这一点，这其实就是题目中的“隐含”的已知条件。
我们的分析过程一般分为五步：
（1）画出每个时刻的等效电路图，并在电路图标出“显性”和“隐性”的已知条件。
（2）运用串并联电路的特点和欧姆定律，列出方程或方程组求解未知量。
用口诀总结解题过程就是：“画等效，标已知，运规律”。
此题有两个时刻，一是“P在a处”时刻，一是“P在b处”时刻。当“P在a处”时，滑动变阻器接入电路中的阻值是0Ω；当“P在b处”时，滑动变阻器接入电路中的阻值为阻值最大值。
解：当S1闭合，S2断开，P在a处时,此时的等效电路图如图14-3-16所示：
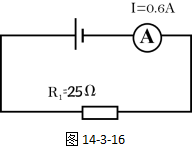
当S1闭合，S2断开，P在 b处时,此时的等效电路图和已知条件如图14-3-17所示：
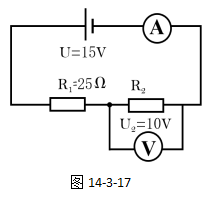
R2的电压与电压表的示数相同，则
则通过R2的电流为
则R2的最大阻值为
答：电源电压为15V，R2的最大阻值为50Ω。
由于通过R2的电流大小并不能通过简单的某个公式可以求出，这时可借助九宫图来计算出未知量。
滑动变阻器的极值问题
在动态电路中，由于用电器的规格、电流表、电压表的量程限制，使得滑动变阻器的滑片在移动过程中也存在限制，滑动变阻器接入电路中的阻值存在最大值和最小值。所谓滑动变阻器的极值问题是指如何求解出动态电路中，滑动变阻器连入电路中的阻值的最大值和最小值问题。
例题：如图14-3-18所示，电源电压6V，滑动变阻器R上标有“1A,20Ω”,电阻R0=10Ω，电流表量程是0~0.6A，电压表的量程是0~3V，求滑动变阻器R接入电路中的阻值范围。
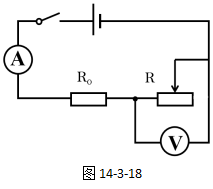
【分析】滑动变阻器接入电路的阻值范围不一定与滑动变阻器的铭牌上标注的阻值范围一致。因此，滑动变阻器接入电路的阻值范围需要重新计算，而不能简单地认为滑动变阻器接入电路中的阻值范围一定与滑动变阻器的铭牌上标注的阻值范围相同。
比如，此题中滑动变阻器铭牌指定的最小阻值为0Ω，如果此时滑动变阻器接入电路中的最小阻值与滑动变阻器铭牌指定的最小阻值相等，则意味着滑动变阻器的接入电路中的阻值为0Ω，则电路中的电流I=U/R0=6V/8Ω=0.75A，超过电流表允许通过最大量程0.6A，可能损坏电流表等。
另外有趣的是，无论是求解滑动变阻器接入电路中的阻值最大值还是最小值，电路的连接方式往往是不会发生有改变的，但这个问题仍可以看成是动态电路问题，因为当分别求解最大值和最小值时，电路中的已知条件是不一样的。
比如说，当求解滑动变阻器接入电路中的阻值最小值时，已知条件是——滑动变阻器允许通过的最大电流值。当求解滑动变阻器接入电路中的阻值最大值时，已知条件是——滑动变阻器允许通过的最大电压值和滑动变阻器的最大铭牌电阻值。
也就是说，无论是求滑动变阻器的最大值，还是最小值，都需要借助一个“已知的最大值”来求解，之所以不利用“已知的最小值”来求解，是因为各元件的“铭牌”最小值一般都为0Ω，而滑动变阻器的滑片在移动过程中，是不可能达到元件的“铭牌”最小值的。
因此，若要求解求解滑动变阻器的阻值最小值时，已知的最大值只能是先求出通过滑动变阻器的最大电流；当求解滑动变阻器的阻值最大值时，已知的最大值却有两个，一个是滑动变阻器的铭牌值；一个是滑动变阻器的两端允许的最大电压值。
上述解题思路用口诀总结为：“欲求极值，先知最大；求阻小看大流，求阻大看铭阻与滑压”。这句口诀的含义是：如果要求解滑动变阻器的最大值和最小值，需要先获知一些最大值的物理量来计算。比如在计算滑动变阻器的最小值时，先判断出电路中的最大电流是多少；在计算滑动变阻器的最大值，不但要看滑动变阻器的铭牌电阻值是多少，还要看滑动变阻器上的电压表的最大量程是多少。
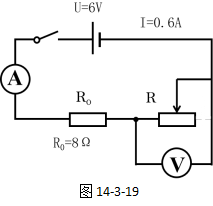
解：（1）当滑动变阻器的最小值时，则滑动变阻器的电流有最大值。
由于电流表允许的最大电流为0.6A，滑动变阻器允许的最大电流为1A，因此，电路允许的最大电流取0.6A，即滑动变阻器的最大电流也为0.6A，则此时的等效电路图及已知条件情况如图14-3-19所示。
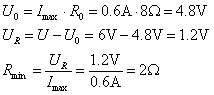
（2）当滑动变阻器的最大值时，则滑动变阻器的电压表的示数取最大值。由图中的已知条件可知，
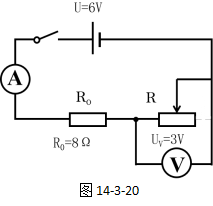
由于电压表允许的最大电压为3V，则此时的等效电路图及已知条件情况如图14-3-20所示。
由图中的已知条件可知，
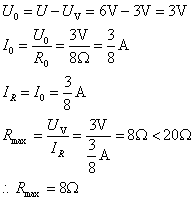
答：滑动变阻器的阻值范围为2Ω~8Ω。
通过这道题，我们发现，确定电路的最大电流不是通过什么公式算出来的，而是通过比较各元件允许的最大电流值进行比较，并运用“大中取小”的原则确定电路的最大电流为多少。为了有效地发现如何通过电路电流最大值求解出滑动变阻器接入电路中的最小值，我们可采用九宫图法（具体见14.2）来实现。
在求解滑动变阻器的最大阻值时，如果有电压表测量滑动变阻器的电压，则意味着通过电压表的最大量程值可求解出滑动变阻器的最大值。为了有效地发现如何通过电压表的最大量程值可求解出滑动变阻器接入电路中的最大值，我们仍可采用九宫图法（具体见14.2）来实现。
需要注意的是，通过电压表的最大量程值可求解出滑动变阻器接入电路中的最大值后，还需要与滑动变阻器的铭牌最大电阻值进行比较，并运用“大中取小”的原则确定滑动变阻器接入电路中的最终的最大阻值是多少。
在求解滑动变阻器接入电路中的最大阻值时，如果没有电压表测量滑动变阻器的电压，那么情况就变得简单多少了，滑动变阻器允许接入电路中的最大阻值就是滑动变阻器铭牌中标注的最大阻值。
为了有效地发现如何通过电流最大值求解出滑动变阻器最小值或如何通过滑动变阻器两端的最大电压值求解出滑动变阻器的最大值，我们可采用九宫图法来实现。
【本节我们学到的内容】
1、测算小灯泡电阻的原理是什么
2、测算小灯泡电阻的实验使我们得到一个什么样的结论
灯泡的电阻随温度的升高而增大。
3、测算小灯泡电阻的实验中常见的电路故障现象及原因
（1）电流表无示数，电压表有示数（接近电源电压）——电压表的测量对象断路。
（2）电流表有示数，电压表无示数——电压表的测量对象短路。
4、串联分压定律的内容及公式
在串联电路中，电阻大的分压多。
5、并联分流定律的内容及公式
在并联电路中，电阻大的通过的电流反而小。
6、动态电路的计算技巧
口诀：“画等效，标已知，运规律”。
7、滑动变阻器的极值问题
口诀总结为：“欲求极值，先知最大；求阻小看大流，求阻大看铭阻与滑压”。
【自我检测与巩固】
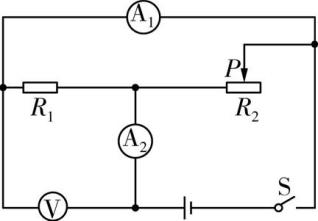
1、如图所示,电源电压不变,闭合开关S,将滑动变阻器的滑片P从中点向右滑动,下列说法中正确的是( )
A.电流表A1的示数变小
B.电压表V的示数变大
C.电流表A2的示数与电流表A1的示数的差值变大
D.电压表V的示数与电流表A2的示数的比值变大
2、如图所示，是定值电阻R和小灯泡L中电流随电压变化的图象，由图象可知( )
A．乙是小灯泡的IU图象
B．定值电阻的阻值为5 Ω
C．定值电阻R和小灯泡L并联接在4 V的电源上，干路中的电流是1.2 A
D．定值电阻R和小灯泡L串联接在6 V的电源上，电路中的电流是0.4 A
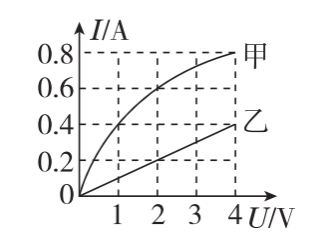
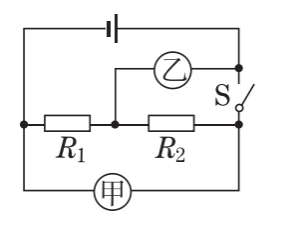
3、如图所示，已知R1：R2＝3：1，当开关S闭合，甲、乙两表为电压表时，两表示数之比U甲：U乙＝________；当开关S断开，甲、乙两表为电流表时，两表示数之比I甲：I乙＝________。
4、某实验小组用伏安法测量待测电阻Rx的阻值，设计的实验电路如图甲所示。
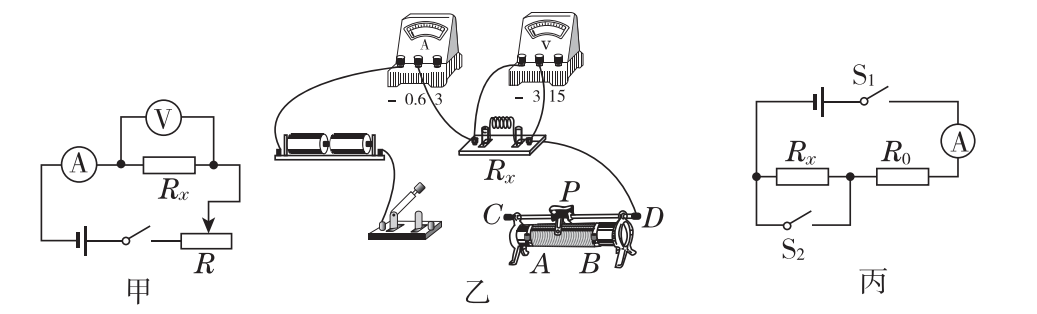
(1)根据图甲用笔画线代替导线将图乙的实物图补充完整。
(2)该实验的原理是________。
(3)某次测量时，电压表的示数为1.5 V，电流表的示数为0.3 A，则待测电阻的阻值为________Ω；实验时应多测几组数据，求电阻的平均值，目的是________。
(4)若撤去电压表和滑动变阻器，新增一个阻值为R0的定值电阻，利用如图丙所示的实验电路，也可以测量待测电阻Rx的阻值。实验步骤如下：
①首先，闭合开关S1、S2，记录电流表的示数I1；
②接着，断开开关________，记录电流表的示数I2；则待测电阻的阻值Rx＝________(用R0、I1、I2表示)。
5、在如图所示的电路中，电源电压保持不变，电阻R1的阻值为30 Ω，闭合开关S1，断开开关S2，电流表A1的示数为0.3 A；闭合开关S1和S2，电流表A2的示数为1.2 A。
求：(1)电源电压U。(2)电阻R2的阻值。
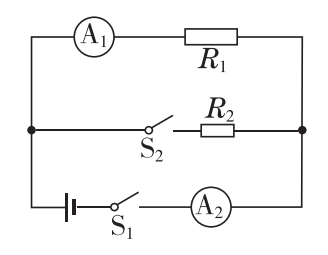
6、如甲所示，当开关S从点2转到1时，电流表和电压表对应的示数如图乙所示，由图甲和图乙中的信息请解答：
(1)电源电压是多少？
(2)S接1时，R1的电阻是多少？
(3)S接2时，R2的电阻是多少？
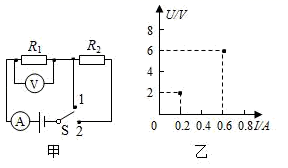
7、如图所示电路，电源电压不变，R2=20Ω ， R3=30Ω。当S1闭合，S2断开时，电流表的示数为0.4A。当S1， S2都断开时，电流表的示数为0.3A。求：
(1)电源电压；
(2) R1阻值；
(3)当S1，S2都闭合时，电流表的示数。
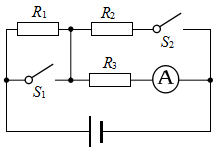
8、标有“5 Ω 0.8 A”的定值电阻R1和标有“20 Ω 0.5 A”的滑动变阻器R2连接在如图所示的电路中，其中电源电压为4.5 V，电流表的量程为0～0.6 A，电压表的量程为0～3 V。闭合开关，在保证电路安全的情况下，滑动变阻器的阻值调节范围是多少？
Was this helpful?
1 / 0
