一、角
转动就是研究这个角度随时间的变化。
角度随时间变化,就像一维情况下讨论的“位置”和 “速度”相似,在平面转动中相应讨论“角位置”和“角速度”。
二维的转动和一维位移之间存在着一个联系,几乎每一个量都有它的对应量。
转过的角度θ相当于物体移动的距离y。
角速度是指一秒钟内角度的变化有多大。
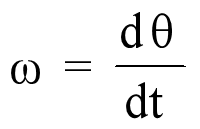
正如一维空间物体在一秒钟内走了多远,即速度v。
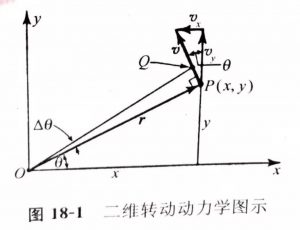
如上图,由P点转动至Q点,转过的角度为△θ,PQ的长度则为r·△θ,PQ在x坐标轴上的投影△x则代表了在转动过程中,位置P在x坐标轴上的变化。也就是说,PQ可用x坐标轴上的△x和y坐标轴上的△y来表示(有了△x和△y,再通过平行四边形法则得到PQ)。
通过三角计算,我们发现了如下等式:
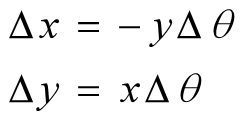
假如物体是以一定的角速度ω转动的,用△t去除上式的两边,得到

通过将上面两式的速度合成,可得
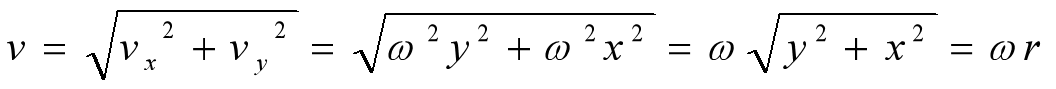
二、转矩
现在,我们来通过转动时做功情况来得出一个转矩概念。
有一个力作用作用在转动的刚体上,此刚体绕一根轴转动。将这个力分解为Fx和Fy ,则这个力对刚体转过△θ时所做功为:
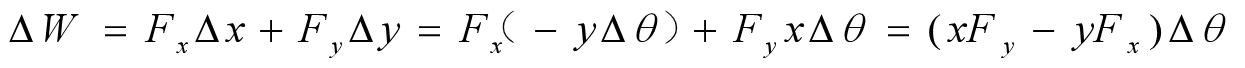
我们将上式中括号内的部分称为转矩,之所以称为转矩,用符号τ表示(发音为涛)。因为它与角度相乘得到了功,这有些类似一维动力学中,力与距离的乘积为功。转矩就相当于一维动力学中的“力”,角度相当于“距离”。
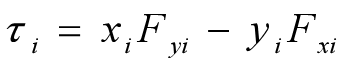
因此,功的改变等于各个不同的作用力产生的所有的转矩之和与△θ的乘积。
转矩的公式还有其他的写法,如图
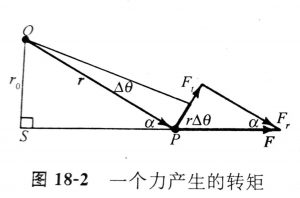
不考虑x和y坐标轴,只考虑力F与原点至质点的距离r的夹角α,我们也可得到一个由做功得到转矩的推导公式
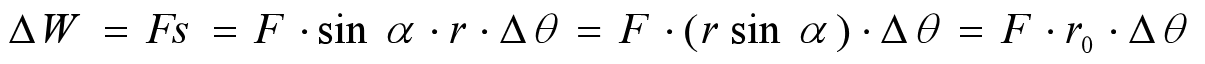
也就说是,转矩的第三个公式为
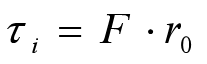
转矩的大小反映了转动物体的能力,它随力臂增大而变大。所以,矩其实是一种力的作用通过“力臂”的大小来倍数加权。
转动微妙之处在于,将位移分解成一种常量距离与动态角的乘积,或者说,动态角是一种修正系数,常量距离通过乘以动态角这个修正系数才能形成真正的在力的方向上通过了一段距离。
所以,力乘以在力的方向上通过的距离才是做功,而矩虽然看形式上也是力与某种距离的乘积,但上述任何一种公式可以看出,矩是力与垂直距离的乘积,这种乘积还不如看成力的倍数加权,仍属于一个矢量,不是能量的形式。
三、角动量
在一维运动学中,外力(合力不为零)是一群质点的总动量p的变化率。也是动量变化的原因。
类似的,外转矩是一群质点的角动量L的变化率,也是角动量变化的原因。
Was this helpful?
0 / 0