将新的时空坐标轴(也可叫飞船坐标系)与旧的时空坐标轴(也可叫地球坐标系)合在一起
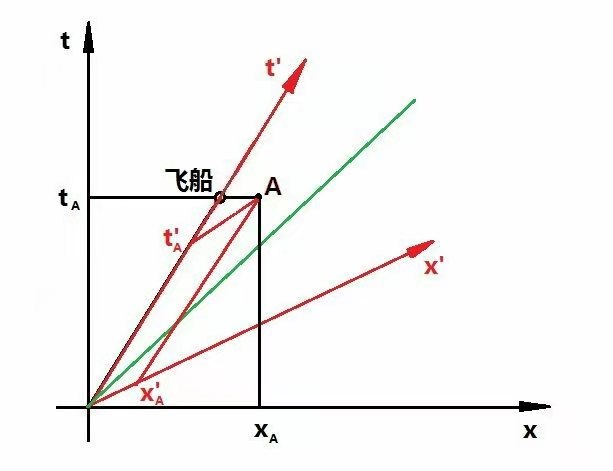
从图中,我们发现,新的空间时间坐标系其实是旧的空间时间坐标系的转动形成的(只不过这种坐标系的转动遵循的是相对论的洛仑兹变换方程组,所以说,洛仑兹变换类同一种坐标系转动,不过这是一种空时系的“转动”)。
【编者评:个人觉得,千万不要认为,地球上看到的客体与在飞船上看到的同一客体有可能不同。其实两个系统分别看一物体,其实是一样的,只不过为两个系统放在一起联系起来时,描述同一事件时,所用的物理量之间要进行类似旋转的变换。】
飞船的速度u越快,则x’与t’越向世界线x=t靠拢。
我们有个矢量(比如动量),这个矢量可以分成x,y,z三个坐标的空间矢量的分量。但是第四个量,在空间转动下看起来像一个普通的标量,因为只要我们所处的系统如果不是处于运动坐标系中,它总是不变的。
但是,当我们观察的物体可在不同的参照系出现时,相当于坐标系按照洛仑兹变换规律旋转时,时间分量t与空间分量(x,y,z)是一样会发生改变的。
那么,的确存在这样的一个情况:动量的三个分量和作为时间分量的能量一起变换,就构成了一个所谓的“四维矢量”。
现在,我们来论证为什么动量是空间分量,能量是时间分量。
我们知道,有关能量与质量关系的公式如下:
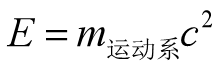
根据“质能相当”,能量与质量只相差一个因子c2,我们知道,弹簧的弹力公式F=kx,形变大小x其实就代表了力F的大小,我们甚至可将形变大小看成是力的等价效果的表现。
同理,我们也可将质量m代表了总能量E,质量大小看成是能量大小产生的等价效果。
通过推导,在相对飞船的物体所具有的能量E’和动量p’与相对地球的物体所具有的能量E和动量p的变换推导过程如下:

我们清楚地看到
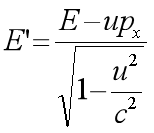
与
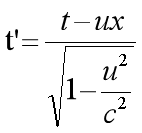
何其的相似。
不难同理推导出
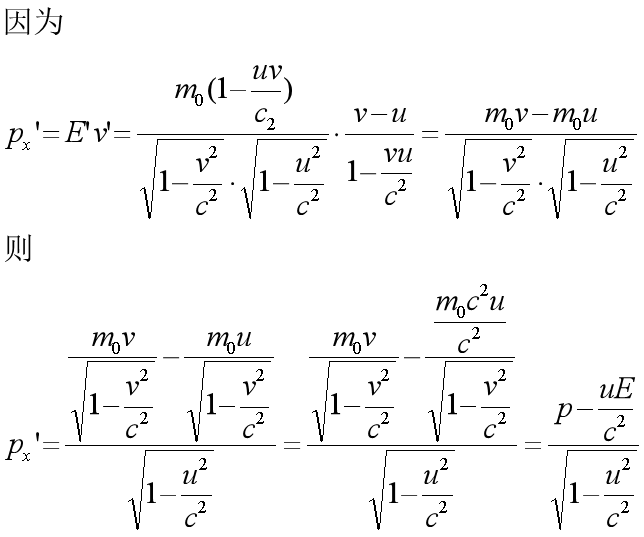
由此可见,用原来的能量和动量来表示新的能量与动量的变换与用t和x来表示t’及用用t和x来表示x’的变换是完全一样的。
也就是说,空间轴变成动量分量轴,时间轴变成能量轴,类似新的时间量度是由旧的时间量度与旧的空间量度的混合,新空间的动量也是旧空间的动量与旧空间的能量的混合。
动量是一个四维矢量。
在一般的转动问题中,我们发现,有一个变的量x2+y2+z2。在四维问题中,我们也发现相应的不变的量是:t2-x2-y2-z2。这个不变的式子代表什么呢?对于动量,换一种形式可写成
E2-p2=m02
四维动量矢量的长度平方等于m02
【编者评:能量E与动量p其实都可以看成能量,一种是空间能量,一种是时间能量。由于动量是矢量,所以是线的形式来展现它们大小之间的关系。】
如果静止质量m0为零,例如光子。如果光子像粒子,带有一定量的能量和动量。由于能量E=hυ,动量p=h/λ,所以光子的能量一定是动量乘以c,E=pc,或者,如果c=1,则能量与动量相等。这就是说,静止质量为零。
光没有静止质量,这意味着它永远以光速运动才具有能量。也就是,光不可能静止下来,静止下来就不是光了。
对于光而言,不同的频率意味着有不同的能量。
Was this helpful?
0 / 0