7.2 怎样比较运动的快慢
【与教材不同之处】
更巧妙引入速度概念;更详细总结了对匀速和变速直线运动的图像特征;更详细描述了平均速度概念。
谁游得快
假如我们是观众,根据如图7-2-1所示,三位运动员中哪位运动员游得最快?
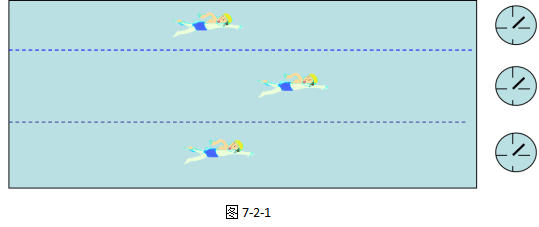
显然,中间的运动员游得最快。
那么,这样判断的依据是什么呢?
你可能会说,中间的同学游在最前面。说的没错,在物理上,游在最前面的叫做“通过的路程最大”。
如果你足够仔细的话,你还会发现,图中右边有记录时间的钟表,这些钟表的示数是一样,说明三位运动员虽然通过的路程不一样,但所用的时间是一样的。
显然,如果不控制三位运动员所用的时间相同,只比较通过的路程大小来判断哪位运动员游得最快就毫无意义了。
所以,当通过比较路程来判断不同物体运动的快慢时,前提条件是不同物体运动时所用时间必须相同,于是我们得到这么一个判断物体运动快慢的方法:相同时间内,物体通过的路程越长,则物体运动得越快。
我们可以用简单的话来概括上面的方法,即“相同时间比路程”。
我再看一张图,根据如图7-2-2所示,三位运动员中哪位运动员游得最快?
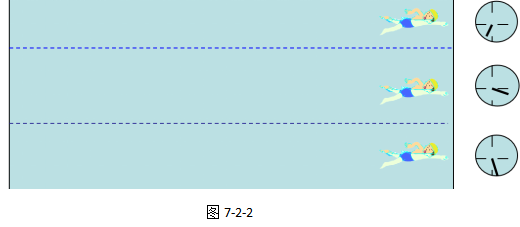
我们仔细观察图中右边记录时间的钟表的示数,我们发现中间的运动员所用的时间最少。此时我们再也不能通过比较路程的方法来判断三位运动员中哪位运动员游得最快了,但并不意味着没有其他办法了。
显然,在通过相同路程的情况下,所用时间是最小的,就是游得最快的。
所以,我们还可以通过“相同路程比时间”的方法来判断物体运动的快慢——当通过的路程相同时,物体花费的时间越少,则物体运动得越快。
裁判就是采用这种方法来判断哪位运动游得最快。
所以,我们现在有两种比较物体运动快慢的两种方法:相同时间比路程;相同路程比时间。
比较快慢的第三种方法
如图7-2-3所示,假如小汽车在120s内行驶3600m,越野车在200s内行驶4000m,这两辆车运动的时间不同,通过的路程也不相同,这意味着我们再也不能直接通过“相同时间比路程”或“相同路程比时间”的方法来判断哪辆车行驶得更快?
那么我们如何比较它们的快慢呢?

同样,我们再用越野车通过的路程与所用时间进行比值计算,我们也将得到越野车在1s内通过的路程是多少?如果我们用小汽车通过的路程与所用时间进行比值计算,我们将得到小汽车在1s内通过的路程是多少?
我们的计算过程如下:
![]()
![]()
计算结果显示:小汽车1s内通过的路程是30m,越野车1s内通过的路程是20m。
根据“相同时间比路程”方法,我们可以立即判断出小汽车运动得更快。
其实,我们已经找到了第三种比较物体运动快慢的方法——比值法,即求解路程与时间的比值,比值越大,则物体运动得越快。
不难发现,这种利用“路程与时间的比值”来判断物体运动的快慢,本质上仍是采用了“相同时间比路程”方法。
于是,我们不难进一步推断出:利用“时间与路程的比值”也是可以判断出物体运动的快慢的,因这“时间与路程的比值”本质上仍是采用“相同路程比时间”的方法。
由于“路程与时间的比值”越大,则意味着物体运动得越快,相比“时间与路程的比值”越小,则意味着物体运动得越快而言,更易于被人们接受,所以,当我们使用比值的方法来判断物体运动的快慢时,往往采用“路程与时间的比值”来反映物体运动的快慢。
什么是速度
物理学上,将“路程与时间的比值”称为速度,符号是v。
速度越大,表示物体运动得越快,所以,速度是反映物体运动快慢的物理量。
根据定义,我们得到的速度公式如下:
![]()
用物理量符号表示上述公式:
![]()
其中,s表示路程,t表示时间,v表示速度。
由速度的公式可以推知,速度的单位可以是一个复合单位,由长度单位和时间单位共同组成。由于长度的国际制单位是米(m),时间的国际制单位是秒(s),所以,速度的国际制单位是米/秒,单位符号是m/s。
速度还有一个非常常用的单位:千米/时,单位符号是km/h。
两个单位的换算是:
![]()
我们试着推导一下,这个换算关系是如何得到的:
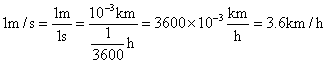
同学们,请思考行人步行速度是1.5km/h的物理意义是什么?
请完成这个填空:1.5km/h的物理意义是指行人 1 ____ 内通过的路程是1.5 ____ 。
跟速度有关的计算
将公式
![]()
变形,可以得到另外两个变形公式:
![]()
![]()
这两个公式分别用于求解物体运动一段路程后所用的时间t及物体运动的路程s。
例题:气象预报称,台风中心正以7m/s的速度向距其126km的某地接近。请你算一下,台风中心需要多长时间到达该地?
【分析:物理计算题解题格式包含5要素:已知、求、解、公式、答。在“已知”中,必须用规定的物理符号表示题中的已知量,单位可在这一步中换算统一。】
已知:v=7m/s=25.2km,s=126km
求:t
解:![]()
答:台风中心需要6小时到达该地。
匀速直线运动与变速直线运动
物体做机械运动,按照运动轨迹的曲直可分为直线运动和曲线运动。
在直线运动中,按照速度是否改变,又分为匀速直线运动和变速直线运动。
物理学上,在任意相同时间内通过的路程相等,这样的运动称为匀速直线运动。
在物理学上,在相同时间内通过的路程不相等,这样的运动称为变速直线运动。
如图7-2-4中甲图为匀速直线运动,乙图为变速直线运动。
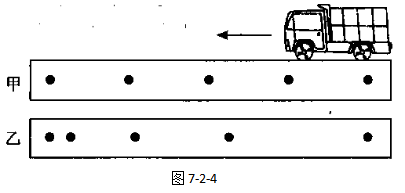
在生活中,比如一个人乘坐自动扶梯以不变的速度的上楼,就属于匀速直线运动。而一个熟透的苹果从树上竖直落下,虽然苹果落下时的运动方向没变,但由于它的下落速度会随着时间的推移越来越大,所以,苹果下落是变速直线运动,如图7-2-5所示。

匀速直线运动与变速直线运动的图像
匀速直线运动和变速直线运动的坐标图像一般有两种,分别是速度-时间图(v-t图)和路程-时间图(s-t图)。
图7-2-6所示的是v-t图像,图中水平的甲直线表示速度始终保持10m/s不变,属于匀速直线运动;倾斜的乙直线表示的是速度从0m/s开始,随着时间的推移,速度越来越大,在4s时乙的速度达到了20m/s,属于变速直线运动。
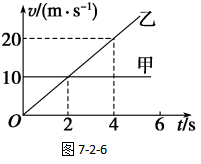
v-t图的优点是可以直接看出物体的速度大小,通过v-t图我们还可以方便地直观地了解物理量之间的关系。通过7-2-6图,我们可以知道,当物体作匀速直线运动时,它通过的路程和所用的时间都在增大,但它的速度没有发生改变,这说明匀速直线运动的物体,它的速度大小与路程、时间都是无关的。所以,匀速直线运动物体的v-t函数关系的数学图像是“一条平行于横轴的直线”。静止物体的v-t函数关系的数学图像是“横轴”。
v-t图的缺点是路程的大小需要进行计算。
比如,请求解上图中甲在4s内的通过的路程是多少?
【分析:解题过程中如果题目出现了两个以上的物理过程,公式中的各物理量还要标上“下标”以示区分。】
已知:v甲=10m/s t=4s
解:![]()
答:甲在4s内的通过的路程是40m。
所以,甲的速度比乙的速度大,从图像上看,速度大的甲所在的直线的倾斜程度更大,乙所在的直线的倾斜程度相比之下,显得平缓一些。
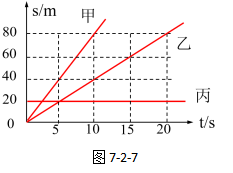
图7-2-7所示的是s-t图像,我们先观察甲的运动图像——一条倾斜的直线。通过分析这条直线经过的坐标点,我们发现,每隔5秒,甲通过距离都是40米,即相同的时间间隔内,甲车通过的距离总是相等的,这说明甲在做匀速直线运动。同理,每隔5s,乙通过距离都是20m,这说明乙也在做匀速直线运动。
丙在0s时已经有了一定的路程20m,在20s时,它的路程大小仍是20m,这说明,丙的运动状态是静止。
所以,匀速直线运动s-t函数关系的数学图像是“一条斜直线”。静止物体的s-t函数关系的数学图像是“与横轴平行直线或横轴”。
s-t图的优点是可以直接看出物体通过的路程大小,缺点是速度大小不能直观地看出,需要通过利用公式计算出来。
利用图像比较速度的大小
由于s-t图不能直接得到速度的大小,所以,利用s-t图比较两个物体的速度大小时可利用一些技巧。
比如,图7-2-8中甲车和乙车,在0-5s的时间内,哪辆车的速度更大?
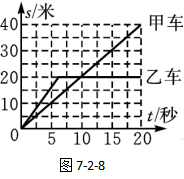
分析:假如我们沿竖直方向画一条线,该线经过5秒,则意味着甲车、乙车都行驶了5s,这时我们可以发现,甲车通过的路程是10米,乙车通过的路程约15米。根据相同时间内,通过的路程越大的,则运动得越快,我们可以判断出甲车的速度小,乙车的速度大。
什么是平均速度
变速直线运动比较复杂,如果只是做些粗略的研究。我们将物体在一段时间内通过的总路程与总时间的比值来计算它的速度,这样计算出来的速度叫平均速度。
所以,平均速度的求解公式是:
![]()
用符号表示公式:

需要注意的是,平均速度与速度的平均是完全不同的两个概念。速度的平均是指两个速度的平均值,而平均速度是总路程与总时间的比值,两者不能混为一谈。
平均速度在计算题中的应用
例题:利用图7-2-8提供的信息,请求出乙车在0-20秒内的平均速度。
【分析:乙在前7秒左右,保持匀速直线运动;在7-20秒时,乙车是处于静止状态。看似情况非常复杂,其实求乙车的平均速度,根本不需要关注乙车的具体的运动过程发生什么了变化,只要知道整个过程的总路程是多少就可以了,显然,整个过程的乙车通过的路程是20米。】
已知:s总=20m t总=20s
求:平均速度v
解: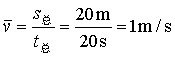
答:乙车在0-20秒内的平均速度是1m/s。
我们再看一个例题。
例题:某位同学参加百米赛跑,前50m的平均速度是7m/s,后50m的平均速度是8m/s,请求出整个过程中该同学的跑步速度是多少?
【分析:此题看似简单,好像只要将7m/s和8m/s相加后再除以2,便可以求出平均速度了。其实这样求出的结果不是平均速度,而是速度的平均值。要求出整个过程的平均速度,必须先获知总路程和总时间是多少。该题的难点在于总时间没有直接告诉我们,需要我们先求出跑完前50m和后50m所用的时间各是多少,再两段时间相加便可得到总时间的大小。】
已知:s总=100m v1=7m/s v2=8m/s
求:v
解:
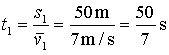
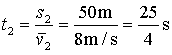
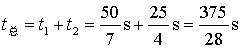
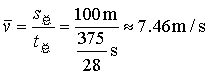
所以
答:整个过程中该同学的跑步速度约7.46m/s。
【本节学到的内容】
1、比较物体运动快慢的三种方法分别什么?
(1)相同时间内,物体通过的路程越长,则物体运动得越快。
(2)当通过的路程相同时,物体花费的时间越少,则物体运动得越快。
(3)求解路程与时间的比值,比值越大,则物体运动得越快。
2、什么是速度?
物理学上,将“路程与时间的比值”称为速度,符号是v。
公式:![]()
国际制单位:m/s
常用单位:km/h
两者的换算:1m/s=3.6km/h
3、什么是匀速直线运动与变速直线运动?
物理学上,在任意相同时间内通过的路程相等,这样的运动称为匀速直线运动。它的特点是:在任何相等的时间内,通过的路程都相等。
在物理学上,在相同时间内通过的路程不相等,这样的运动称为变速直线运动。它的特点是:在相等的时间内,通过的路程并不相等。
4、匀速直线运动在v-t图像与s-t图像中的特点
v-t图像中,匀速直线运动是“一条平行于横轴的直线”。
s-t图像中,匀速直线运动是“一条斜直线”,且倾斜程度越大,所代表的速度越大。“平行于横轴的直线”代表物体处于静止状态。
5、什么是平均速度
一段时间内通过的总路程与总时间的比值来计算它的速度,这样计算出来的速度叫平均速度。公式:
【作业检测与巩固】
1、在下列图象中能表示物体匀速直线运动的是( )
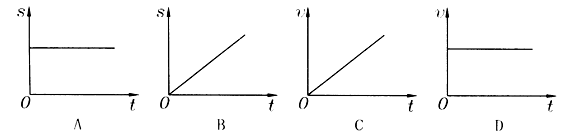
2、甲、乙两物体都做直线运动,通过的路程之比是3:1,所用的时间之比是2:3,则甲、乙两物体运动的平均速度之比是________。
3、物体做匀速直线运动,路程与时间的关系图像如图所示,由图可知,甲、乙两运动物体的速度大小关系是( )

A、v甲 > v乙
B、v甲 < v乙
C、v甲 = v乙
D、条件不足,不能确定
4、做变速直线运动的物体,前一半路程的平均速度为4m/s,后一半路程的平均速度为6m/s,它在整个过程中的平均速度是多少?
Was this helpful?
1 / 0